Bisectriz de un triángulo

Una bisectriz de un ángulo es una línea recta trazada desde el vértice de un triángulo hasta su lado opuesto, de tal manera que divide el ángulo en dos ángulos iguales o congruentes.

Teoremas de la bisectriz del ángulo de los triángulos

La siguiente tabla muestra las afirmaciones relacionadas con los teoremas de la bisectriz interna y externa de los ángulos, así como su inversa:

Teorema de la bisectriz del ángulo interno

La bisectriz de un ángulo de un triángulo divide el lado opuesto en dos partes proporcionales a los otros dos lados del triángulo.

Inverso del teorema del bisector del ángulo interno

En un triángulo, si el punto interior es equidistante de los dos lados de un triángulo, entonces ese punto se encuentra en la bisectriz del ángulo formado por los dos segmentos de recta.

Teorema de la bisectriz perpendicular

La mediatriz divide el segmento de recta dado en dos partes iguales, a las que es perpendicular. En un triángulo, si se traza una mediatriz desde el vértice hasta el lado opuesto, se divide el lado en dos segmentos congruentes.

Teorema de la bisectriz externa del ángulo

La bisectriz externa del ángulo divide externamente el lado opuesto en la proporción de los lados que contienen el ángulo, y esta condición suele darse en triángulos no equiláteros.

Bisectriz perpendicular

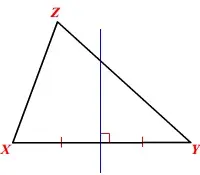
La mediatriz de un lado de un triángulo es una línea perpendicular al lado que pasa por su punto medio.

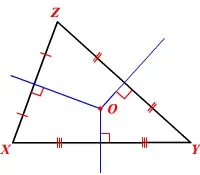
Las tres mediatrices de los lados de un triángulo se encuentran en un único punto, llamado circuncentro. Un punto en el que se cruzan tres o más rectas se llama punto de concurrencia. Así, el circuncentro es el punto de concurrencia de las bisectrices de un triángulo.

Aquí, O es el circuncentro de Δ X Y Z .

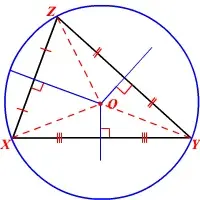
El circuncentro es equidistante de los vértices del triángulo. (Ver teorema del circuncentro.) Es decir, X O = Y O = Z O . La circunferencia dibujada con el circuncentro como centro y el radio igual a esta distancia pasa por los tres vértices y se llama circunferencia . Es la circunferencia más pequeña en la que se puede inscribir el triángulo.

El circuncentro se encuentra dentro del triángulo para los triángulos agudos, en la hipotenusa para los triángulos rectos y se encuentra fuera del triángulo para los triángulos obtusos. El circuncentro coincide con el punto medio de la hipotenusa si se trata de un triángulo rectángulo isósceles.

• Las casas de Natha, Hiren y Joe representan tres puntos no colineales en un plano de coordenadas. Si quieren reunirse en un lugar común de forma que cada uno tenga que recorrer la misma distancia desde sus casas, ¿cómo se decide el punto de encuentro?

Como los puntos que representan las casas no son colineales, los tres puntos forman un triángulo.

Ahora bien, si consideras el circuncentro del triángulo, éste será equidistante de los vértices. Es decir, si se elige como punto de encuentro el circuncentro del triángulo formado por las tres viviendas, cada uno tendrá que recorrer la misma distancia desde su casa.

• Hallar el valor de x .

Aquí, O es el punto de concurrencia de las tres bisectrices perpendiculares de los lados de Δ K L M .

Por tanto, O es el circuncentro del triángulo.

El circuncentro es equidistante de los vértices. Entonces, O M = O K .

Es decir, 6 x + 1 = 19 .

Resolver para x .

6 x + 1 - 1 = 19 - 1 6 x = 18 6 x 6 = 18 6 x = 3

Vídeos de Bisectriz de un triángulo