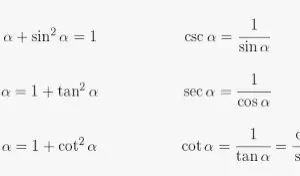Calcular ángulos de un triangulo
Suma de los ángulos interiores de un polígono de n lados
180 (n-2) grados
Halla la suma de todos los ángulos interiores utilizando esta fórmula y réstale la suma de todos los ángulos conocidos para encontrar el ángulo interior desconocido.
sin, cos y tan
sin θ = opuesto / hipotenusa
cos θ = adyacente / hipotenusa
tan θ = opuesto / adyacente
Utiliza una de estas razones trigonométricas en función de los dos lados disponibles para encontrar el ángulo desconocido.
Ley de los senos
a/sin A = b/sin B = c/sin C
Aquí, A, B y C son los ángulos de un triángulo y a, b y c son sus respectivos lados opuestos.
La ley de los senos se utiliza para encontrar ángulos desconocidos cuando se nos dan
a) dos lados y un ángulo no incluido (o)
b) dos ángulos y un lado no incluido.
Ley de los cosenos
a2 = b2 + c2 - 2bc cos A
b2 = c2 + a2 - 2ca cos B
c2 = a2 + b2 - 2ab cos C
Aquí, A, B y C son los ángulos de un triángulo y a, b y c son sus respectivos lados opuestos.
La ley de los cosenos se utiliza para hallar los ángulos desconocidos cuando nos dan con
a) tres lados (o)
b) dos lados y el ángulo incluido.
Ejemplos que utilizan la fórmula para encontrar ángulos
- Encuentra el quinto ángulo interior de un pentágono si cuatro de sus ángulos interiores son 108°, 120°, 143° y 97°.
Solución:
El número de lados de un pentágono es, n = 5.
La suma de los 5 ángulos interiores de un pentágono = 180 (n -2)° = 180 (5 - 2)° = 540°.
La suma de los 4 ángulos interiores dados = 108°+ 120°+ 143°+ y 97°= 468°.
Por tanto, el quinto ángulo interior = 540° - 468° = 72°.
Respuesta: El quinto ángulo interior del pentágono dado = 72°.
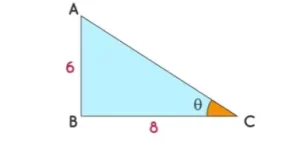
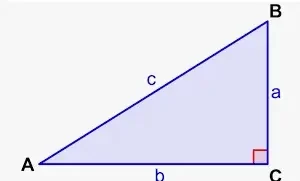
- Encuentra el ángulo en el vértice C del siguiente triángulo utilizando una de las fórmulas para encontrar ángulos. Redondea tu respuesta al número entero más cercano.
Encontrar los ángulos que faltan en un triángulo
Solución:
Encontrar: El ángulo en C que es θ.
Se da que AB = 6 = Lado opuesto de θ.
BC = 8 = Lado adyacente de θ.
- Como conocemos tanto los lados opuestos como los adyacentes de θ, utilizamos la fórmula de tan θ para hallar θ.
tan θ = opuesto/adyacente
tan θ = 6/8 = 0,75
θ = tan-1 (0,75)
Usando la calculadora,
θ ≈ 37° (redondeado al entero más cercano).
Respuesta: El ángulo en C es, θ = 37°
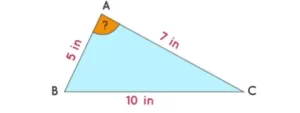
- Encuentra el ángulo en el vértice A del siguiente triángulo utilizando una de las fórmulas para encontrar ángulos. Redondea tu respuesta a las décimas más cercanas.
Solución:
Hallar: El ángulo en A.
- Sabemos que los lados opuestos a A, B y C están representados por a, b y c respectivamente. Así que tenemos:
a = 10 in; b = 7 in; y c = 5 in.
Como conocemos los tres lados, tenemos que utilizar la ley de los cosenos para encontrar el ángulo en A.
a2 = b2 + c2 - 2bc cos A
102 = 72 + 52 - 2 (7)(5) cos A
100 = 49 + 25 - 70 cos A
100 = 74 - 70 cos A
70 cos A = 74 - 100
70 cos A = -26
cos A = -26 / 70
A = cos-1 (-26/70)
Utilizando la calculadora,
A ≈ 111,8° (redondeado a la décima más cercana).
Respuesta: El ángulo en A = 111,8°
Vídeos de Calcular ángulos de un triangulo
Entradas Relacionadas
Contenido