Continuidad en un punto

En cálculo, una función es continua en x = a si -y sólo si- se cumplen las tres condiciones siguientes:

• La función está definida en x = a; es decir, f(a) es igual a un número real
• El límite de la función cuando x se aproxima a a existe
• El límite de la función a medida que x se acerca a a es igual al valor de la función en x = a

Hay tres tipos básicos de discontinuidades:

• Discontinuidad removible (puntual): la gráfica tiene un agujero en un solo valor de x. Imagina que vas caminando por la calle y alguien ha quitado la tapa de una alcantarilla (¡Cuidado, no te caigas!). Esta función cumplirá la condición #2 (el límite existe) pero no la condición #3 (el límite no es igual al valor de la función).
• Discontinuidad infinita - la función va hacia el infinito positivo o negativo. Imagínese una carretera que se acerca cada vez más a un río sin puente al otro lado
• Discontinuidad de salto - la gráfica salta de un lugar a otro. Imagina a un superhéroe que va de paseo: llega a un callejón sin salida y, como puede, vuela a otra carretera.
• Tanto la discontinuidad infinita como la discontinuidad en salto fallan la condición #2 (el límite no existe), pero la forma en que fallan es diferente. Recordemos que para que exista un límite, los límites izquierdo y derecho deben existir (ser finitos) y ser iguales. Las discontinuidades infinitas tienen límites izquierdo y derecho infinitos. Las discontinuidades de salto tienen límites izquierdo y derecho finitos que no son iguales.

Ejemplo de continuidad en un punto

Gran parte del análisis de límites está relacionado con un concepto conocido como continuidad. Se dice que una función es continua en un intervalo cuando la función está definida en cada punto de ese intervalo y no sufre interrupciones, saltos o rupturas. Si alguna función f(x) satisface estos criterios desde x=a hasta x=b, por ejemplo, decimos que f(x) es continua en el intervalo [a, b]. Los paréntesis significan que el intervalo es cerrado, es decir, que incluye los puntos extremos a y b. En otras palabras, que el intervalo se define como a ≤ x ≤ b. Un intervalo abierto (a, b), en cambio, no incluiría los puntos extremos a y b, y se definiría como a < x < b.

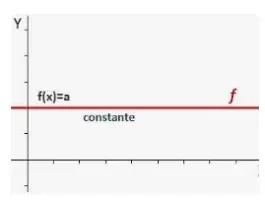
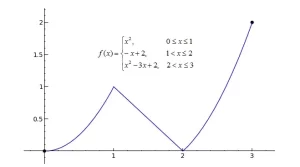
Para un ejemplo de continuidad, inicia una nueva hoja de trabajo llamada 02-Continuidad, y luego recrea la siguiente gráfica usando el código proporcionado. (La f(x)=... está superpuesta).

Vídeos de Continuidad en un punto

https://www.youtube.com/watch?v=Yb-lUhwxRKA