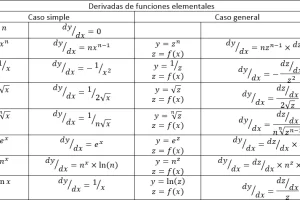
Reglas de la derivada

Las reglas de la derivada en el Cálculo se utilizan para encontrar las derivadas de diferentes operaciones y diferentes tipos de funciones como las funciones de potencia, las funciones logarítmicas, las funciones exponenciales, etc. Todas estas reglas se obtienen a partir de la definición de límite de la derivada por la cual la derivada de una función f(x) (denotada por f '(x)) viene dada por el límite:

La derivada de una función y = f(x) se escribe como f'(x) (o) dy/dx (o) d/dx (f(x)) y da la pendiente de la curva en un punto fijo. También da la tasa de cambio de una función con respecto a una variable. Algunas reglas importantes de la derivada son

• Regla de la potencia
• Regla de la suma/diferencia
• Regla del producto
• Regla del cociente
• Regla de la cadena

Reglas de diferenciación de diferentes funciones

Veamos las reglas de diferenciación de diferentes tipos de funciones. Si quieres ver la demostración de cada regla de derivación, haz clic en el enlace correspondiente.

Reglas de derivación de las funciones exponenciales

La función exponencial es una función cuya base es una constante y cuyo exponente es una variable. Existen principalmente dos tipos de funciones exponenciales: ex y ax, donde 'e' es el número de Euler y 'a' es una constante cualquiera. Vamos a ver las reglas de las derivadas de las funciones exponenciales.

La derivada de ex es, d/dx (ex) = ex.
La derivada de ax es, d/dx (ax) = ax ln a.

Reglas de derivación de funciones logarítmicas

Una función logarítmica implica un logaritmo (común o natural), es decir, es de la forma logₐ x (o) ln x. Las reglas para encontrar las derivadas de estas dos funciones logarítmicas son:

La derivada de logₐ x es, d/dx (logₐ x) = 1 / (x ln a)
La derivada de ln x es, d/dx (ln x) = 1/x.

Reglas de derivación de las funciones trigonométricas

Tenemos seis funciones trigonométricas: sen, cos, tan, csc, sec y cot. Aquí están las reglas para encontrar las derivadas de las funciones trigonométricas.

La derivada de sen x es, d/dx (sen x) = cos x
La derivada de cos x es, d/dx (cos x) = - sin x
La derivada de tan x es, d/dx (tan x) = sec2x
La derivada de csc x es, d/dx (csc x) = - csc x cot x
La derivada de sec x es, d/dx (sec x) = sec x tan x
La derivada de cot x es, d/dx (cot x) = - csc2x

Reglas de derivación de las funciones trigonométricas inversas

Hay 6 funciones trigonométricas inversas correspondientes a las funciones trigonométricas anteriores. Recuerda que las derivadas de las funciones trigonométricas inversas NO implican ninguna función trigonométrica/trigonométrica inversa. Estas son las reglas:

La derivada del seno inverso es, d/dx (sen-1x) = 1/√(1-x2)
La derivada del coseno inverso es, d/dx (cos-1x) = -1/√(1-x2)
La derivada del tan inverso es, d/dx (tan-1x) = 1/(1 + x2)
La derivada de cosec inverso es, d/dx (csc-1x) = -1/ [x √(x2 - 1) ], x ≠ 1, -1, 0
La derivada del sec inverso es, d/dx (sec-1x) = 1/ [x √(x2 - 1) ], x ≠ 1, -1, 0
La derivada de la cot inversa es, d/dx (cot-1x) = -1/(1 + x2)

Reglas de derivación de las funciones hiperbólicas

Hay 6 funciones hiperbólicas que corresponden a 6 funciones trigonométricas. Cada función trigonométrica seguida de una "h" es su correspondiente función hiperbólica. Aquí están las derivadas de las funciones hiperbólicas.

La derivada de sinh x es, d/dx (sinh x) = cosh x
La derivada de cosh x es, d/dx (cosh x) = sinh x
La derivada de tanh x es, d/dx (tanh x) = sech2 x
La derivada de csch x es, d/dx (csch x) = - csch x coth x
La derivada de sech x es, d/dx (sech x) = - sech x tanh x
La derivada de coth x es, d/dx (coth x) = - csch2 x

Reglas de derivación de las funciones hiperbólicas inversas

Hay de nuevo 6 funciones hiperbólicas inversas que corresponden a 6 funciones hiperbólicas. Aquí están las reglas para encontrar sus derivadas.

La derivada de sinh-1x es, d/dx (sinh-1x) = 1/√(1+x2)
La derivada de cosh-1x es, d/dx (cosh-1x) = 1/√(x2-1), x>1
La derivada de tanh-1x es, d/dx (tanh-1x) = 1/(1-x2), |x|<1
La derivada de csch-1x es, d/dx (csch-1x) = -1/ [ |x| √(1-x2) ], x ≠ 0
La derivada de sech-1x es, d/dx (sech-1x) = -1/ [ x√(1-x2) ], 0 < x < 1
La derivada de coth-1x es, d/dx (coth-1x) = 1/(1-x2), |x|>1

Vídeos de Reglas de la derivada