Diagonal de un cuadrado
Un cuadrado es una forma geométrica que está totalmente determinada por las longitudes de sus lados, a. Si conocemos la longitud del lado de un cuadrado, conocemos su perímetro, su área, la longitud de sus diagonales, etc.
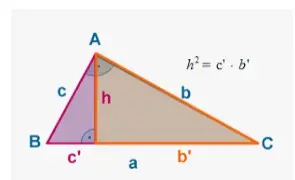
En geometría, un cuadrado es un cuadrilátero regular que tiene cuatro lados de igual longitud y cuatro ángulos que miden 90 grados. Un cuadrado puede tener dos diagonales. Cada una de las diagonales puede formarse uniendo los vértices del cuadrado que son diagonalmente opuestos. La longitud de la diagonal de un cuadrado se puede calcular mediante el teorema de Pitágoras. El teorema de Pitágoras se simplifica reconociendo que las longitudes de los lados necesarios son iguales.
La diagonal de un cuadrado es un segmento de línea que une dos vértices no adyacentes. Un cuadrado tiene dos diagonales que tienen la misma longitud y se bisecan en ángulo recto. La fórmula de la diagonal del cuadrado se utiliza para calcular la longitud de la diagonal de un cuadrado cuando se conoce la longitud de sus lados.
¿Qué es la diagonal de un cuadrado?
Un cuadrado tiene dos diagonales y cada diagonal se forma uniendo los vértices opuestos del cuadrado. Observa el siguiente cuadrado para relacionarlo con las propiedades de las diagonales que se dan a continuación.
- Las diagonales de un cuadrado tienen la misma longitud.
- Son bisectrices perpendiculares entre sí.
¿Qué es la fórmula de la diagonal del cuadrado?
La fórmula de la diagonal de un cuadrado, es d = a√2; donde 'd' es la diagonal y 'a' es el lado del cuadrado. La fórmula de la diagonal de un cuadrado se deriva utilizando el teorema de Pitágoras. Una diagonal divide un cuadrado en dos triángulos rectángulos isósceles. Ambas diagonales son congruentes y se bisecan en ángulos rectos. Vamos a entender cómo derivar la fórmula para encontrar la diagonal de un cuadrado.
Fórmula de la diagonal de un cuadrado
Consideremos el triángulo ADC en el cuadrado. Sabemos que todos los ángulos de un cuadrado son de 90°, por lo tanto, utilizando el teorema de Pitágoras, podemos encontrar la hipotenusa, que es 'd' en este caso.
d2 = a2 + a2
d = √(a2 + a2)
d = √(2a2)
d = √2 × √a2
= √2a
Vídeos de Diagonal de un cuadrado
Entradas Relacionadas
Contenido