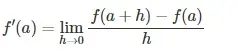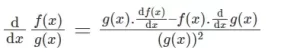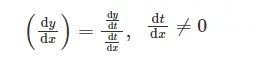Diferencial de una función

Si f es una función de valor real y 'a' es cualquier punto de su dominio para el que f está definida, entonces se dice que f(x) es diferenciable en el punto x=a si la derivada f'(a) existe en todos los puntos de su dominio. Viene dada por:

Dado que este límite existe y f'(a) representa la derivada de f(x) en a. Este es el primer principio de la derivada.
El dominio de f'(a) se define por la existencia de sus límites. La derivada también se denota como:

Si y = f(x) entonces la derivada de f(x) viene dada como d/dx o y'.

Esto se conoce como derivada de y con respecto a x.

También, la derivada de una función f en x en x = a está dada como:

La derivada de una función f(x) significa la tasa de cambio de la función f(x) con respecto a x en un punto situado en su dominio. Para que una función sea diferenciable en cualquier punto x = a de su dominio, debe ser continua en ese punto concreto, pero lo contrario no siempre es cierto.

Álgebra de las derivadas

El proceso de determinar la derivada de una función se conoce como diferenciación. Es claramente visible que el concepto básico de derivada de una función está estrechamente relacionado con los límites. Por lo tanto, es de esperar que las reglas de las derivadas sean similares a las de los límites. Las siguientes reglas forman parte del álgebra de las derivadas:

Consideremos que f y g son dos funciones de valor real tales que la diferenciación de estas funciones está definida en un dominio común. Entonces,

La suma de las derivadas de las funciones f y g es igual a la derivada de su suma, es decir

Sea u = f(x) y v = g(x), entonces (u + v)' = u' + v'

La diferencia de las derivadas de las funciones f y g es igual a la derivada de la diferencia de estas funciones, es decir

Sea u = f(x) y v = g(x), entonces (u - v)' = u' - v'

La derivada del producto de dos funciones f y g viene dada por la regla del producto, es decir

Sea u = f(x) y v = g(x), entonces la regla del producto puede replantearse como

(uv)' = u'v + uv'

También se conoce como regla de Leibnitz para diferenciar productos de funciones

La derivada del cociente de dos funciones f y g viene dada por la regla del cociente (siempre que el denominador sea distinto de cero), es decir

Sea u = f(x) y v = g(x), entonces la regla del cociente se puede reformular como

Regla de la cadena:

Cuando una cantidad 'y' varía con otra cantidad 'x' de forma que y = f(x), entonces f'(x) indica la tasa de cambio de y con respecto a x (en x = x0). Además, si dos variables 'x' e 'y' varían con respecto a una tercera variable, digamos 't', entonces, según la regla de la cadena, tenemos

Vídeos de Diferencial de una función