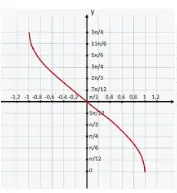
Dominio arcotangente

El arctán es la inversa de la función tangente y se utiliza para calcular la medida del ángulo a partir de la relación de tangencia de un triángulo rectángulo, designada por la fórmula

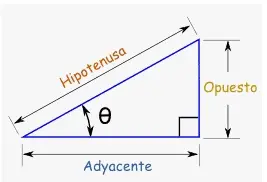
tan = opuesto / adyacente

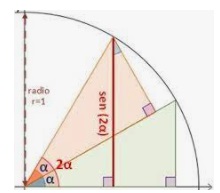
El término 'arco' se utiliza porque al medir un ángulo en radianes, la longitud del arco de una porción de un círculo bisecado por un ángulo (con el vértice en el centro del círculo) es igual a la medida del ángulo. El radián es la unidad de medida estándar de un ángulo y equivale aproximadamente a 57 grados. Se basa en el radio de un círculo.

Fórmula de la tangente inversa

En trigonometría, cada función como el seno, el coseno y la tangente tiene su función inversa. La fórmula de la tangente se utiliza para hallar el tan de un ángulo en un triángulo rectángulo. La fórmula de la tangente inversa se utiliza para encontrar el ángulo cuando conocemos el lado opuesto a ese ángulo y el lado adyacente. La inversa de la tangente se representa por arctan o tan-1.

Las funciones/cocientes trigonométricas son:

• Seno
• Coseno
• Tangente
• Secante
• Cosecante
• Cotangente

Las inversas de estas funciones trigonométricas son las siguientes

• seno inverso
• coseno inverso
• tangente inversa
• secante inversa
• cosecante inversa
• cotangente inversa

Cuándo utilizar Arctan

Las funciones trigonométricas pueden utilizarse para definir valores relacionados con un triángulo rectángulo. En la práctica, estas funciones pueden utilizarse para determinar alturas de objetos o distancias que son difíciles de medir. Estas medidas se determinan utilizando la medida de un ángulo (no el ángulo recto) y una razón de dos lados del triángulo. Las funciones trigonométricas están determinadas por los lados del triángulo que se utilizan en la relación de estas fórmulas:

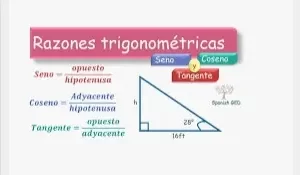
• seno = opuesto / hipotenusa
• coseno = adyacente / hipotenusa
• tangente = opuesto / adyacente

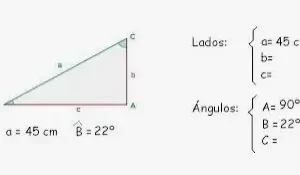
La inversa de estas funciones se puede utilizar para determinar las medidas de los ángulos cuando se conocen los lados del triángulo. Se puede utilizar el arctán para determinar la medida de un ángulo cuando se conocen el lado opuesto y el lado adyacente al ángulo. El arctán tiene aplicaciones prácticas en arquitectura, construcción, paisajismo, física e ingeniería, entre otras áreas científicas y matemáticas.

Propiedades de Arctan x

A continuación se presentan algunas identidades arctanas útiles basadas en las propiedades de la función arctana. Estas fórmulas se pueden utilizar para simplificar expresiones trigonométricas complejas, aumentando así la facilidad de intentar los problemas.

• tan (tan-1x) = x, para todos los números reales x
• tan-1x + tan-1y = tan-1[(x + y)/(1 - xy)], cuando xy < 1
• tan-1x - tan-1y = tan-1[(x - y)/(1 + xy)], cuando xy > -1
• Tenemos 3 fórmulas para 2tan-1x
• 2tan-1x = sin-1(2x / (1+x2)), cuando |x| ≤ 1
• 2tan-1x = cos-1((1-x2) / (1+x2)), cuando x ≥ 0
• 2tan-1x = tan-1(2x / (1-x2)), cuando -1 < x < 1
• tan-1(-x) = -tan-1x, para todo x ∈ R
• tan-1(1/x) = cot-1x, cuando x > 0
• tan-1x + cot-1x = π/2, cuando x ∈ R
• tan-1(tan x) = x, sólo cuando x ∈ R - {x : x = (2n + 1) (π/2), donde n ∈ Z}
  es decir, tan-1(tan x) = x sólo cuando x NO es un múltiplo impar de π/2. En caso contrario, tan-1(tan x) es indefinido.

Vídeos de Dominio arcotangente

https://www.youtube.com/watch?v=vJnn6Cjzx_s