Ecuación de la parábola

La sección de un cono circular recto por un plano paralelo a una generatriz del cono es una parábola. Es un lugar de un punto, que se mueve de manera que la distancia a un punto fijo (foco) es igual a la distancia a una línea fija (directriz)

Ecuación estándar de la parábola

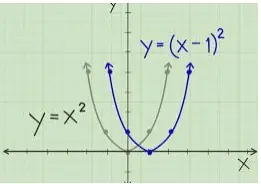
La ecuación más sencilla de una parábola es y2 = x cuando la directriz es paralela al eje y. En general, si la directriz es paralela al eje y en la ecuación estándar de una parábola viene dada como

y2 = 4ax

Si la parábola es lateral, es decir, la directriz es paralela al eje x, la ecuación estándar de una parábola pasa a ser

x2 = 4ay

Además de estas dos, la ecuación de una parábola también puede ser y2 = 4ax y x2 = 4ay si la parábola está en los cuadrantes negativos. Así, las cuatro ecuaciones de una parábola vienen dadas como

y2 = 4ax
y2 = - 4ax
x2 = 4ay
x2 = - 4ay

Derivación de la ecuación de la parábola

En la ecuación anterior, "a" es la distancia del origen al foco. A continuación se presenta la derivación de la ecuación de la parábola. En primer lugar, consulta la imagen que aparece a continuación.

Recto de la parábola

El latus rectum de una parábola es la cuerda que pasa por el foco y es perpendicular al eje de la parábola.

Coordenadas paramétricas de la parábola

Para una parábola, la ecuación es y2 = -4ax. Ahora, para representar las coordenadas de un punto de la parábola, la forma más sencilla será = at2 e y = 2at ya que para cualquier valor de "t", las coordenadas (at2, 2at) siempre satisfarán la ecuación de la parábola, es decir, y2 = 4ax. Por lo tanto,

Cualquier punto de la parábola

y2 = 4ax (at2, 2at)

Vídeos de Ecuación de la parábola