Fórmula de polígonos regulares
En función de la medida del ángulo y de los lados de un polígono, éste se clasifica en
- Polígono regular - Todos los ángulos interiores y los lados tienen la misma medida
- Polígono irregular - Todos los ángulos interiores y los lados tienen valores diferentes
- Polígono convexo - Todos los ángulos interiores de un polígono < 180 grados
- Polígono cóncavo - Polígonos que tienen uno o más ángulos interiores con una medida de >180 grados
El número de lados de un polígono determina su forma y recibe el nombre de su número de lados. Ejemplos comunes de polígonos son los triángulos, cuadrados, pentágonos, hexágonos, etc.
¿Qué es la fórmula del polígono?
Las fórmulas importantes asociadas a un polígono regular se dan a continuación:
- Fórmula 1: Para un polígono regular de "n" lados, la suma de los ángulos interiores de un polígono es 180°(n-2)
- Fórmula 2: El número de diagonales de un polígono de "n lados" = [n(n-3)]/2
- Fórmula 3: La medida de cada ángulo interior de un polígono regular de n lados = [(n-2)180°]/n
- Fórmula 4: La medida de los ángulos exteriores de un polígono regular de n lados = 360°/n
Propiedades del polígono
Las propiedades importantes del polígono son
- La suma de los ángulos interiores de todos los cuadriláteros = 360°.
- Si al menos uno de los ángulos interiores es > 180º, se denomina polígono cóncavo.
- Si un polígono no se cruza a sí mismo y sólo tiene un límite, se llama polígono simple. En caso contrario, se trata de un polígono complejo.
Ejemplos con fórmulas de polígonos
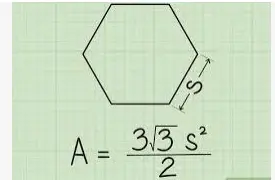
- Encontrar la suma del ángulo interior de un hexágono.
Solución:
Sabemos que un hexágono tiene seis lados.
Usando la fórmula de los polígonos, sabemos que la suma de los ángulos interiores está dada por
Suma de ángulos interiores = 180°(n-2)
= 180°(6-2)
= 180° (4)
= 720°
Por tanto, la suma de los ángulos interiores de un hexágono es 720°.
- Un polígono es un octógono y su longitud de lado es de 7 cm. Calcula el perímetro y el valor de un ángulo interior.
Solución:
El polígono es un octógono. Por tanto, n = 8
Longitud de cada lado, s = 7 cm
El perímetro del octógono es P = n × s
P = 8 × 7
= 56 cm
Ahora, para hallar cada ángulo interior, se utiliza la fórmula del polígono,
Ángulo interior = [(n-2)180°]/n
= [(8 - 2)180°] / 8
= (6 × 180°) / 8
= 135°
Así, el perímetro del octógono dado es de 56 cm y el valor de cada ángulo interior es de 135 grados.
- Utilizando la fórmula del polígono, halla la suma del ángulo interior de un triángulo.
Solución:
Sabemos que un triángulo tiene tres lados.
Usando la fórmula del polígono, sabemos que la suma de los ángulos interiores viene dada por:
Suma de ángulos interiores = 180°(n-2)
= 180°(3-2)
= 180° (1)
= 180°
Por lo tanto, la suma de los ángulos interiores de un triángulo es 180°.
Vídeos de Fórmula de polígonos regulares
Entradas Relacionadas
Contenido