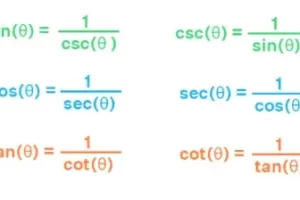Fórmula del seno
En trigonometría, la función seno puede definirse como la relación entre la longitud del lado opuesto y la de la hipotenusa en un triángulo rectángulo. La función seno se utiliza para encontrar el ángulo o los lados desconocidos de un triángulo rectángulo.
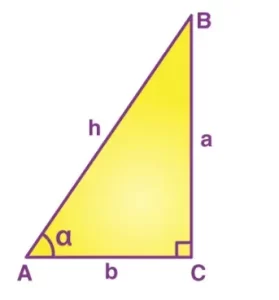
Para cualquier triángulo rectángulo, digamos ABC, con un ángulo α, la función seno será
Sin α= Opuesto/ Hipotenusa
Fórmula de la función seno
En un triángulo rectángulo, el seno de un ángulo es igual a la relación entre el lado opuesto al ángulo (también llamado perpendicular) y la hipotenusa.
Supongamos que 'α' es el ángulo, en un triángulo rectángulo ABC.
Entonces, la fórmula del seno viene dada por:
Sin α= Lado opuesto/ Hipotenusa
o
Sin α = Perpendicular/Hipotenusa
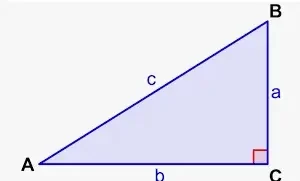
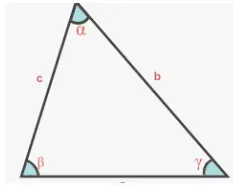
Según la figura dada, la fórmula del seno se convierte en,
Sin α = a/h
donde 'a' es el lado opuesto al ángulo 'α' y 'h' es la hipotenusa.
Propiedades de la función seno según los cuadrantes
La función seno tiene valores positivos o negativos dependiendo de los cuadrantes. En la tabla anterior, se observa que el seno 270 es negativo mientras que el seno 90 es positivo. En el caso de la función seno, el valor depende de los cuadrantes y es positivo para el primer y segundo cuadrante, mientras que es negativo para los valores del tercer y cuarto cuadrante.
Dominio y rango de la función seno
Como sabemos, la función seno está definida para todos los números reales, por lo que el dominio de y = sen x es el conjunto de todos los números reales, es decir, R. El rango de la función seno es el intervalo cerrado [-1, 1]. Es decir, -1 ≤ y ≤ 1 o -1 ≤ sen x ≤ 1. Sin embargo, el rango de esta función se puede dar según los cuadrantes. Observa la siguiente tabla para obtener el rango de la función seno en diferentes cuadrantes.
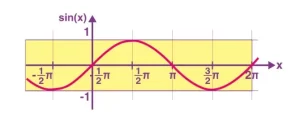
Gráfica de la función seno
La gráfica del seno se parece a la imagen que se muestra a continuación. La gráfica del seno o gráfica sinusoidal es una gráfica de arriba a abajo y se repite cada 360 grados, es decir, en 2π. En el diagrama de abajo, se puede ver que desde 0, la gráfica del seno sube hasta +1 y luego baja hasta -1 desde donde vuelve a subir.
La función y = sen x es una función impar, porque
sin (-x) = -sin x
Identidades de la función seno
Algunas de las identidades comunes del seno son
seno (θ) = cos(π/2 - θ) = 1/cosec(θ)
arcsin (sin θ) = θ, para -π/2 ≤ θ ≤ π/2
cos2 (θ) + sin2 (θ) = 1
Sin (2x) = 2sin (x) cos (x)
Cos (2x) = cos2(x) - sin2(x)
Existen otras identidades del seno. A continuación se indican los valores de otras funciones trigonométricas en términos de seno, que son muy útiles para resolver diversos tipos de preguntas.