Función creciente

Las funciones pueden aumentar, disminuir o permanecer constantes en intervalos a lo largo de todo su dominio. Son continuas y diferenciables en los intervalos dados. Un intervalo se define como una porción continua o conectada en la línea real. Las derivadas se utilizan para identificar si la función dada es creciente o decreciente en un intervalo específico. Por lo tanto, si hablamos gráficamente de que la gráfica de la función va hacia arriba, entonces se llama función creciente. Del mismo modo, si la gráfica va hacia abajo, entonces se llama una función decreciente.

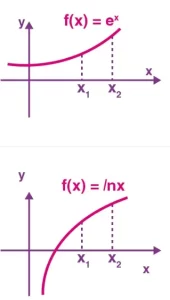
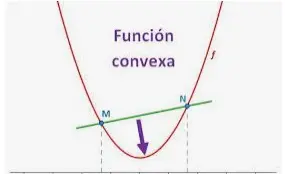
En ambas funciones dadas x1 < x2 y F(x1) < F(x2), por lo que podemos decir que es una función creciente.

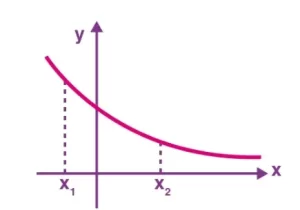
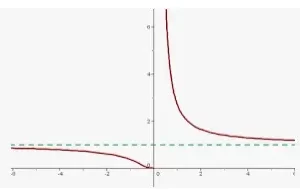
F(x) = e-x

Imaginemos que salimos a dar un paseo. Subimos una colina y observamos que nuestra altura sobre el nivel del mar aumenta a medida que aumenta el tiempo que caminamos. Si consideráramos nuestra altura sobre el nivel del mar, y, como una función de la cantidad de tiempo que estamos caminando, x, diríamos que y aumenta a medida que x aumenta mientras estamos en esa colina.

Sin embargo, siempre es creciente. A veces el camino por el que caminamos va cuesta arriba, a veces cuesta abajo y a veces es plano. Por tanto, en matemáticas, la consideraríamos una función creciente, que aumenta durante ciertos intervalos.

Función estrictamente creciente

Sin embargo, hay funciones que son siempre crecientes. Por ejemplo, imagina que estás en la tienda y compras unas pelotas de béisbol que cuestan 3 dólares cada una. Tu coste total, llámalo c, es una función de cuántas pelotas de béisbol compras, llámalo x, y se puede representar como c(x) = 3x.

Observa que tu coste total siempre aumentará a medida que aumente el número de pelotas de béisbol que compres. Esta función es siempre creciente. Cuando una función es siempre creciente, la llamamos función estrictamente creciente.

¿Qué pasaría si nuestra ruta de senderismo consistiera sólo en tramos llanos y ascendentes sin tramos descendentes? En este caso, seguiríamos diciendo que nuestra función que representa este paseo es creciente, pero todavía no diríamos que es estrictamente creciente. Vamos a explicar esto con más detalle observando las gráficas de las funciones.

Vídeos de Función creciente