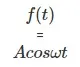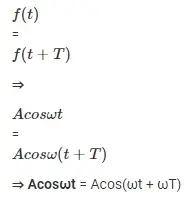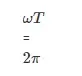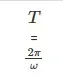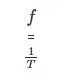Función periódica

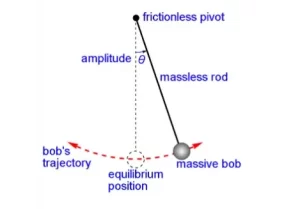
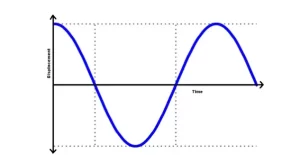
Para entender el concepto de función periódica, consideremos un péndulo que oscila junto con su posición de equilibrio, la trayectoria de la bobina se muestra a continuación, ahora si la bobina está oscilando entonces, su desplazamiento también variará de cero a positivo y de vuelta a cero y negativo, esto se puede ilustrar fácilmente con un gráfico,

Fórmula de la función periódica

Se dice que una función f es periódica si, para alguna constante P no nula, se da el caso de que

f (x+P) = f (x)

Para todos los valores de x en el dominio. Una constante P no nula para la que se da este caso se llama período de la función.

Ecuación de la función periódica

Tomemos el caso de un objeto oscilante, su desplazamiento en movimiento periódico se representa por una función que es periódica en el tiempo;

Tenemos que concentrarnos en los elementos de esta función, la función coseno se repite en el tiempo desde la trigonometría sabemos lo siguiente;

De la ecuación (1) y (2) podemos decir que;

Por lo tanto,

Por lo tanto, el periodo de tiempo del movimiento periódico viene dado por la expresión anterior,
La frecuencia de esta función periódica puede ser dada por el período de tiempo, la frecuencia es el número de oscilaciones por unidad de tiempo, así que si conocemos el tiempo de una oscilación entonces podemos encontrar la frecuencia por:

El movimiento de los planetas alrededor del sol, el movimiento de un yo-yo son ejemplos de funciones periódicas. Aunque el ejemplo del péndulo es un caso especial de función periódica porque ejecuta un movimiento armónico simple, la diferencia radica en cómo se expresa matemáticamente el movimiento. Si la función periódica puede representarse mediante una curva senoidal, entonces se dice que el movimiento es un movimiento armónico simple, como un peso sobre un muelle que oscila, un columpio, etc. El movimiento armónico simple es un tipo de movimiento periódico en el que la fuerza restauradora es directamente proporcional al desplazamiento y actúa en la dirección opuesta a la del desplazamiento.

Vídeos de Función periódica