Derivada arcotangente

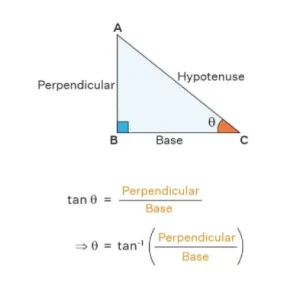
Arctan es una de las funciones importantes de la trigonometría inversa. En un triángulo rectángulo, el tan de un ángulo determina la relación entre la perpendicular y la base, es decir, "Perpendicular / Base". En cambio, el arctán de la relación "Perpendicular / Base" nos da el valor del ángulo correspondiente entre la base y la hipotenusa. Por tanto, arctan es la inversa de la función tan.

Si la tangente del ángulo θ es igual a x, es decir, x = tan θ, entonces tenemos θ = arctan(x). A continuación se presentan algunos ejemplos que pueden ayudarnos a entender cómo funciona la función arctan:

tan(π / 2) = ∞ ⇒ arctan(∞) = π/2
tan (π / 3) = √3 ⇒ arctan(√3) = π/3
tan (0) = 0 ⇒ arctan(0) = 0

Supongamos que tenemos un triángulo rectángulo. Sea θ el ángulo cuyo valor hay que determinar. Sabemos que tan θ será igual al cociente de la perpendicular y la base. Por tanto, tan θ = Perpendicular / Base. Para hallar θ utilizaremos la función arctán como, θ = tan-1[Perpendicular / Base].

Fórmula del arctán

Como se ha comentado anteriormente, la fórmula básica del arctán viene dada por, arctán (Perpendicular/Base) = θ, donde θ es el ángulo entre la hipotenusa y la base de un triángulo rectángulo. Utilizamos esta fórmula para arctan para encontrar el valor del ángulo θ en términos de grados o radianes. También podemos escribir esta fórmula como θ = tan-1[Perpendicular / Base].

Identidades de Arctan

Hay varias fórmulas arctanas, identidades arctanas y propiedades que son útiles para resolver sumas simples y complicadas en trigonometría inversa. A continuación se indican algunas de ellas:

arctan(-x) = -arctan(x), para todo x ∈ R
tan (arctan x) = x, para todos los números reales x
arctan (tan x) = x, para x ∈ (-π/2, π/2)
arctan(1/x) = π/2 - arctan(x) = arccot(x), si x > 0 o,
arctan(1/x) = - π/2 - arctan(x) = arccot(x) - π, si x < 0
sin(arctan x) = x / √(1 + x2)
cos(arctan x) = 1 / √(1 + x2)

También tenemos ciertas fórmulas arctanas para π. Se dan a continuación.

π/4 = 4 arctan(1/5) - arctan(1/239)
π/4 = arctan(1/2) + arctan(1/3)
π/4 = 2 arctan(1/2) - arctan(1/7)
π/4 = 2 arctan(1/3) + arctan(1/7)
π/4 = 8 arctan(1/10) - 4 arctan(1/515) - arctan(1/239)
π/4 = 3 arctan(1/4) + arctan(1/20) + arctan(1/1985)

Dominio y rango de Arctan

Todas las funciones trigonométricas, incluida tan (x), tienen una relación de muchos a uno. Sin embargo, la inversa de una función sólo puede existir si tiene una relación de uno a uno y sobre. Por esta razón, el dominio de tan x debe ser restringido, de lo contrario la inversa no puede existir. En otras palabras, la función trigonométrica debe restringirse a su rama principal, ya que sólo deseamos un valor.

El dominio de tan x se restringe a (-π/2, π/2). Se han excluido los valores en los que cos(x) = 0. El rango de tan (x) son todos los números reales. Sabemos que el dominio y el rango de una función trigonométrica se convierten en el rango y el dominio de la función trigonométrica inversa, respectivamente. Así, podemos decir que el dominio de tan-1x son todos los números reales y el rango es (-π/2, π/2). Un hecho interesante es que podemos extender la función arctan a los números complejos. En tal caso, el dominio de arctan será todos los números complejos.

Vídeos de Derivada arcotangente