Interpretación geométrica de la derivada

Derivada significa la tasa de cambio de una variable con respecto a otra. En otras palabras, podemos decir que una derivada de la función es una tasa de cambio instantánea de la función en un punto determinado. Las derivadas se representan matemáticamente de la siguiente manera:

Alternativamente, también utilizamos la siguiente notación para representar las derivadas de una función:

f ' (x)

Podemos tomar tantas derivadas de funciones diferenciables como sea posible. Cuando tomamos la derivada de la función original, se conoce como primera derivada. Del mismo modo, cuando diferenciamos aún más la primera derivada, obtenemos una segunda derivada y así sucesivamente. A la segunda, tercera y cuarta derivadas de la función las llamamos derivadas de orden superior. Sabemos que la diferenciación toma la función original como entrada y luego devuelve una derivada como salida.

Sabemos que las gráficas se utilizan en matemáticas para interpretar los patrones o relaciones entre dos variables. La gráfica de una función cambia después de diferenciar una función. Cuando diferenciamos la primera derivada para encontrar la segunda derivada, la gráfica vuelve a cambiar.

Interpretación geométrica

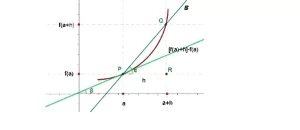
Bien, puede parecer un concepto complejo inicialmente, pero una vez que entiendas el proceso en detalle, te resultará mucho más fácil explicar las derivadas geométricamente. Así, empezaremos con la siguiente figura que representa gráficamente una derivada de la función. Debajo de la figura hemos explicado cómo interpretar o crear esta gráfica en detalle.

Vídeos de Interpretación geométrica de la derivada