Partes de un triángulo

Un triángulo consta de varias partes. Tiene 3 ángulos, 3 lados y 3 vértices. Aprendamos el concepto con la ayuda de la figura de un triángulo que se da a continuación. Observa el triángulo PQR.

Triángulo con ángulos, lados y vértices

En la imagen anterior:

Los tres ángulos son, ∠PQR, ∠QRP, y ∠RPQ.
Los tres lados son el lado PQ, el lado QR y el lado RP.
Los tres vértices son P, Q y R

Clasificación de los triángulos

Según dos elementos principales, los triángulos se pueden clasificar como:

En base a los ángulos

En base a la medida de sus lados

Entendamos la clasificación de los triángulos con la ayuda de la tabla que se presenta a continuación. La tabla ofrece información sobre la diferencia entre 6 tipos diferentes de triángulos en función de los ángulos y los lados.

Nota: La suma de todos los ángulos del triángulo es igual a 180°.

Propiedades del triángulo

Toda forma geométrica tiene propiedades fijas para identificar la relación entre los diferentes lados y ángulos. En esta sección, estudiaremos las propiedades importantes de los triángulos que se enumeran a continuación.

• El triángulo tiene tres lados, vértices y ángulos.
• La propiedad de la suma de ángulos de un triángulo establece que la suma de los tres ángulos interiores de un triángulo es siempre 180°. Por ejemplo, en un triángulo cualquiera PQR, el ángulo P + el ángulo Q + el ángulo R = 180°.
• La propiedad de desigualdad del triángulo establece que la suma de la longitud de los dos lados de un triángulo es mayor que el tercer lado.
• Según el teorema de Pitágoras, en un triángulo rectángulo, el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los otros dos lados, es decir, (Hipotenusa² = Base² + Altitud²).
• El lado opuesto al ángulo mayor es el lado más largo.
• La propiedad del ángulo exterior de un triángulo establece que el ángulo exterior de un triángulo es siempre igual a la suma de los ángulos interiores opuestos.

Fórmulas de los triángulos

En geometría, para cada forma bidimensional, siempre hay dos medidas básicas que necesitamos averiguar, es decir, el área y el perímetro de esa forma. Del mismo modo, el triángulo tiene dos fórmulas básicas que nos ayudan a determinar su área y su perímetro. Veamos las fórmulas en detalle.

Perímetro del triángulo

El perímetro de un triángulo es la suma de los tres lados del triángulo. Consideremos △ABC.

Fórmula del perímetro del triángulo = a + b + c unidades

La mitad del perímetro del triángulo se denomina semiperímetro del triángulo. Se da como (a + b + c)/2 unidades.

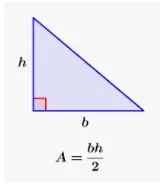
Área de un triángulo

El área de un triángulo es el espacio que cubre el triángulo. Es la mitad del producto de su base y su altura. Siempre se mide en unidades cuadradas, ya que es bidimensional.

Área de ΔABC = 1/2 × AD × BC unidades cuadradas.

Aquí, BC es la base y AD es la altura del triángulo.

Notas importantes sobre el triángulo

• Un triángulo no puede tener una medida o valor de todos los ángulos menor que 60°.
• Un triángulo es una forma cerrada de 3 lados.
• Hay dos fórmulas importantes relacionadas con los triángulos: la fórmula de Herón y el teorema de Pitágoras.
• La suma de los ángulos de un triángulo suma 180° y se da como ∠1 + ∠2 + ∠3 = 180°.

Vídeos de Partes de un triángulo

https://www.youtube.com/watch?v=58f_7Tmxgbg