Perimetro de un polígono regular

La definición del área de un polígono es la medida de la superficie que encierra. Como los polígonos son formas planas cerradas, el área de un polígono es el espacio que ocupa en un plano bidimensional. La unidad del área de cualquier polígono se expresa siempre en unidades cuadradas. Observa la siguiente figura que muestra el área de un polígono en un plano bidimensional.

Fórmulas del área de un polígono

Un polígono se puede clasificar como polígono regular o irregular en función de la longitud de sus lados. Por lo tanto, esta diferenciación también aporta una diferencia en el cálculo del área de los polígonos. El área de algunos polígonos comúnmente conocidos se da como

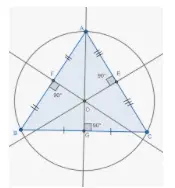
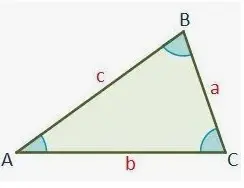
Área del triángulo = (1/2) × base × altura

También podemos encontrar el área de un triángulo si se conoce la longitud de sus lados utilizando la fórmula de Herón que es,

• Área = √s(s-a)(s-b)(s-c), donde s = Perímetro/2 = (a + b + c)/2, a, b y c son la longitud de sus lados.
• Área del rectángulo = longitud × anchura
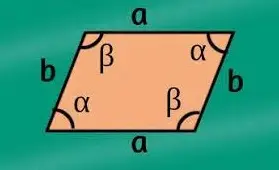
• Área del paralelogramo = base × altura
• Área del trapecio = (1/2) × (suma de las longitudes de sus lados paralelos o bases) × altura
• Área del rombo = (1/2) × (producto de las diagonales)

Para calcular el área de un polígono, primero hay que saber si el polígono dado es un polígono regular o un polígono irregular.

¿Cómo encontrar el perímetro de un polígono?

A partir de la definición de perímetro, éste se define como la suma de la longitud de cada lado. Consideremos, por ejemplo, un cuadrilátero cuyos lados son 12, 6, 8 y 9, el perímetro viene dado por:

Perímetro = 12 + 6 + 7 + 9 = 34

Para un polígono Regular, que tiene todos los lados de igual longitud, el perímetro se define como,

Perímetro = n.s Unidades

donde n = número de lados de un polígono
y s = longitud de un lado

Vídeos de Perímetro de un polígono regular