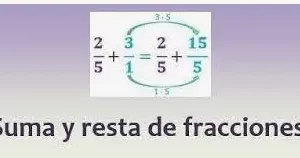
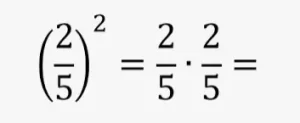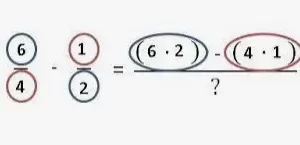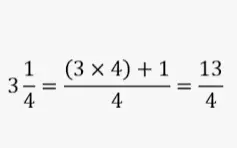Potenciacion de fracciones

Los exponentes fraccionarios son formas de representar potencias y raíces juntas. En cualquier expresión exponencial general de la forma ab, a es la base y b es el exponente. Cuando b se da en forma fraccionaria, se conoce como exponente fraccionario. Algunos ejemplos de exponentes fraccionarios son 21/2, 32/3, etc. La forma general de un exponente fraccionario es xm/n, donde x es la base y m/n es el exponente.

Exponentes fraccionarios

A continuación se dan algunos ejemplos de exponentes fraccionarios muy utilizados:

Exponente Nombre del exponente Indicación
1/2                           Raíz cuadrada        a1/2 = √a
1/3                            Raíz cúbica            a1/3 = 3√a
1/4                            Raíz cuarta            a1/4 = 4√a

Reglas de los exponentes fraccionarios

Hay ciertas reglas a seguir que nos ayudan a multiplicar o dividir números con exponentes fraccionarios fácilmente. Muchas personas están familiarizadas con los exponentes de números enteros, pero cuando se trata de exponentes fraccionarios, acaban cometiendo errores que se pueden evitar si seguimos estas reglas de los exponentes fraccionarios.

Regla 1: a1/m × a1/n = a(1/m + 1/n)
Regla 2: a1/m ÷ a1/n = a(1/m - 1/n)
Regla 3: a1/m × b1/m = (ab)1/m
Regla 4: a1/m ÷ b1/m = (a÷b)1/m
Regla 5: a-m/n = (1/a)m/n

Simplificación de exponentes fraccionarios

La simplificación de los exponentes fraccionarios puede entenderse de dos maneras que son la multiplicación y la división. Se trata de reducir la expresión o el exponente a una forma reducida que sea fácil de entender. Por ejemplo, 91/2 se puede reducir a 3. Vamos a entender la simplificación de exponentes fraccionarios con la ayuda de algunos ejemplos.

1) Resolver 3√8 = 81/3

Sabemos que 8 se puede expresar como un cubo de 2 que se da como, 8 = 23. Sustituyendo el valor de 8 en el ejemplo dado obtenemos, (23)1/3 = 2 ya que el producto de los exponentes da 3×1/3=1. ∴ 3√8=81/3=2.

2) Simplifica (64/125)2/3

En este ejemplo, tanto la base como el exponente están en forma fraccionaria. 64 puede expresarse como un cubo de 4 y 125 puede expresarse como un cubo de 5. Se dan como, 64=43 y 125=53. Sustituyendo sus valores en el ejemplo dado obtenemos, (43/53)2/3. El 3 es una potencia común para ambos números, por lo que (43/53)2/3 puede escribirse como ((4/5)3)2/3, que es igual a (4/5)2, ya que 3×2/3=2. Ahora tenemos (4/5)2, que es igual a 16/25. Por lo tanto, (64/125)2/3 = 16/25.

Vídeos de Potenciacion de fracciones