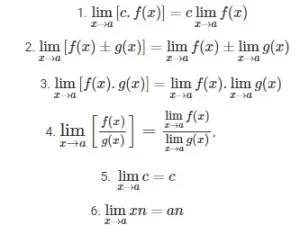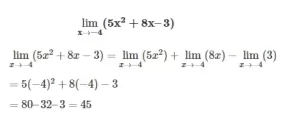Limites

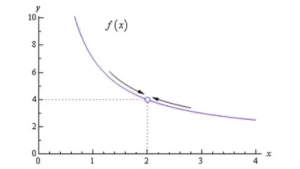
En matemáticas, un límite se define como el valor al que se aproxima una función para los valores de entrada dados. Los límites son importantes en el cálculo y el análisis matemático y se utilizan para definir las integrales, las derivadas y la continuidad. Se utiliza en el proceso de análisis y siempre se refiere al comportamiento de la función en un punto determinado. El límite de una secuencia se generaliza en el concepto de límite de una red topológica y se relaciona con el límite y el límite directo en la categoría de teoría. En general, las integrales se clasifican en dos tipos: integrales definidas e indefinidas. En las integrales definidas, el límite superior y el límite inferior están definidos correctamente. Mientras que en las indefinidas las integrales se expresan sin límites, y tendrá una constante arbitraria al integrar la función.

Propiedades de los limites

Ejemplos de límites

Primero, utiliza la propiedad 2 para dividir el límite en tres límites distintos. A continuación, utilice la propiedad 1 para sacar las constantes de los dos primeros. Esto da,

Como puedes ver, cada una de estas propiedades puede aplicarse a límites bastante complejos para descomponerlos en piezas más pequeñas y sencillas. Cada uno de ellos acabará aplicando una de las dos primeras propiedades enumeradas anteriormente para convertir un límite en algún número. Y al final, acabarás convirtiendo todos los límites en números. En ese momento, podrás manipular todo con álgebra simple para simplificar tu respuesta.

Vídeos de Propiedades de los limites