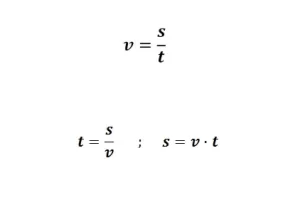Tasa de variación instantánea

Cuando medimos una tasa de cambio en un instante específico en el tiempo, entonces se llama tasa de cambio instantánea. Por otro lado, la tasa de cambio promedio nos hablará de la tasa promedio a la que algún término estuvo cambiando durante algún período de tiempo. Mientras vamos de camino al supermercado, la velocidad cambia constantemente. A veces nos movemos a más de 20 km por hora y otras veces más despacio. En cada instante de tiempo, la tasa de cambio instantánea corresponderá a la velocidad en ese momento exacto.

¿Qué es la tasa de variación instantánea?

La tasa de cambio en un instante o punto de tiempo conocido es la tasa de cambio instantánea. Equivale al valor de la derivada en ese momento concreto. Por lo tanto, podemos decir que, en una función, la pendiente m de la tangente dará la tasa de cambio instantánea en un determinado momento.

Ejemplos resueltos

Q.1: Calcule la tasa de cambio instantánea de la función f(x) dada como

f(x)= 3x² + 12 en x = 5 ?

Solución:

La función dada es

f(x) = 3x² + 12

Hallar su derivada con respecto a x,

f'(x) = 3(2x) + 0

f'(x) = 6x

Por tanto, la tasa de variación instantánea en el punto x = 5 será

f'(5) = 6 × 5

f'(5) = 30

Por lo tanto, la solución es 30.

P.2: Calcula la tasa de cambio instantánea de la función dada como

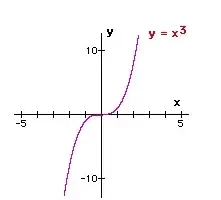
f(x) = 5x³ - 4x² + 2x + 1 en x = 0 ?

Respuesta:

La función dada es:

f(x) = 5x³ - 4x² + 2x + 1

Después de la diferenciación,

f'(x) = 5(3x²) - 4(2x) + 2 + 0

f'(x) = 15x² - 8x + 2

Por tanto, la tasa de variación instantánea en x = 0 será

f'(0) = 2

Por tanto, la solución es 2.

Vídeos de Tasa de variación instantánea

https://www.youtube.com/watch?v=E9e7-NxFFcg