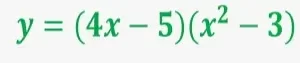Funciones

La mayoría de nosotros ha tenido un trabajo en algún momento de su vida, y lo hacemos para ganar dinero. Piensa en un trabajo en el que te pagan 200 dólares al día. Si sólo trabajas una fracción del día, te llevas esa fracción de 200 dólares. Así, la cantidad total de dinero que ganas en ese trabajo está determinada por el número de días que trabajas.

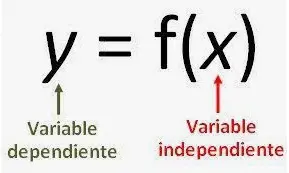
Desde el punto de vista matemático, este escenario es un ejemplo de función. Una función es una relación entre dos variables, de manera que una variable está determinada por la otra. En nuestro ejemplo, si dejamos que x = el número de días que trabajamos e y = la cantidad total de dinero que ganamos en este trabajo, entonces y está determinada por x, y decimos que y es una función de x.

Hemos descrito este ejemplo de función laboral con palabras. También hay otras formas de representar una función. Vamos a ver cómo representar una función con una tabla de funciones, una ecuación y una gráfica.

Representación de funciones

• Algebraicamente
• Numéricamente (representación en tabla)
• Visualmente
• Verbalmente (representación gráfica)

Diferentes tipos de representación de funciones en matemáticas

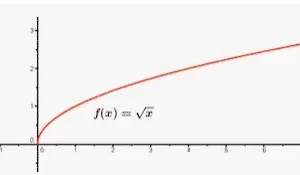
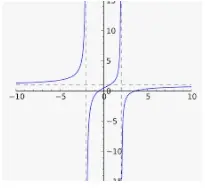
Un ejemplo de función fácil es f(x) = x2. En esta función, la función f(x) toma el valor dado de "x" y lo eleva al cuadrado.Por ejemplo, si x = 3, entonces f(3) = 9. Otros ejemplos de funciones son: f(x) = sen x, f(x) = x2 + 3, f(x) = 1/x, f(x) = 2x + 3, etc.

Hay varios tipos de representación de funciones en matemáticas. Algunos tipos importantes son:

• Función inyectiva o Una a al menos una de las funciones: Cuando existe un mapeo para una variedad para cada dominio entre dos conjuntos.
• Funciones suryectivas o función onto: Cuando hay mapeo de más de un elemento del dominio al rango.
• Función polinómica: La función que está formada por polinomios.
• Funciones inversas: La función que invierte otra función.Estos fueron algunos ejemplos de funciones. Hay que tener en cuenta que hay muchas otras funciones, como la función "into", las funciones algebraicas, etc.

Representación de las funciones

La función es el vínculo entre los dos conjuntos y puede representarse de diferentes maneras. Consideremos el ejemplo anterior de la máquina de imprimir. La función que muestra la conexión entre los números de segundos (x) y por lo tanto los números de líneas impresas (y). Estamos bastante familiarizados con las funciones y ahora descubriremos cómo representarlas.

Representación algebraica de la función

Es una de las representaciones estándar de las funciones. En ella, las funciones se representan explícitamente mediante fórmulas. Las funciones se denotan generalmente con letras minúsculas del alfabeto.

Vídeos de Representación de funciones