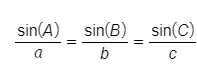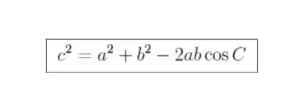Teorema del seno y coseno

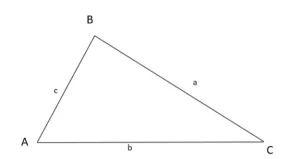
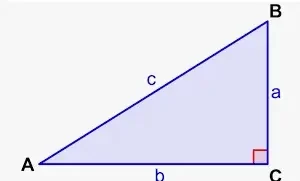
Como vemos a continuación, siempre que etiquetamos un triángulo, etiquetamos los lados con letras minúsculas y los ángulos con letras mayúsculas. Los ángulos y lados opuestos se etiquetan con la misma letra.

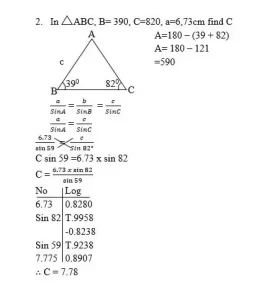
La regla del seno

Para un triángulo con la forma anterior, la fórmula de la regla del seno se define como:

Podemos interpretar la regla del seno así: la relación entre la longitud del lado y el ángulo opuesto es constante en cualquier triángulo. Utilizamos la regla del seno cuando intervienen dos ángulos y dos longitudes. Hay dos situaciones en las que utilizaremos la regla del seno:

• Cuando hay dos ángulos y un lado dados, y necesitamos encontrar la longitud de otro lado.
• Cuando hay dos longitudes y un ángulo dados, y necesitamos encontrar otro ángulo.

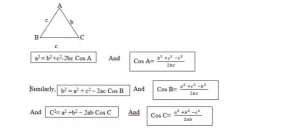
La ley de los cosenos

Hay otras dos versiones de la ley de los cosenos,

a2 = b2 + c2 - 2bc cos A

y

b2 = a2 + c2 - 2ac cos B

Como las tres versiones sólo se diferencian en el etiquetado del triángulo, basta con verificar una sola de ellas.

Ejemplo del teorema del seno y coseno

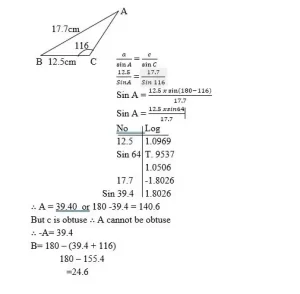
Ley del seno

Encontrar los ángulos restantes de ABC en el que a= 12,5cm, C= 17,7cm y C= 1160

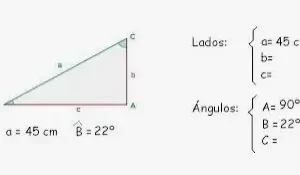
Ley del coseno

La regla del coseno, al igual que la regla del seno, se utiliza para resolver las incógnitas de un triángulo. La regla del coseno se utiliza especialmente para resolver triángulos con la siguiente dimensión.

Vídeos de Teorema del seno y coseno

https://www.youtube.com/watch?v=IwaNWAuQ_Kw