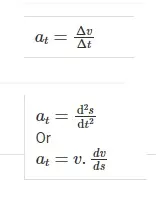Aceleración tangencial
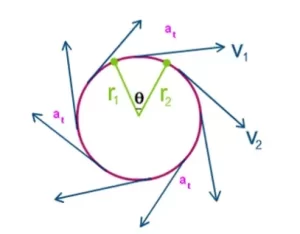
Fórmula de aceleración tangencial: En un movimiento circular, una partícula puede acelerar o frenar o moverse con velocidad constante. Cuando la partícula está en movimiento circular, siempre tendrá una aceleración hacia el centro llamada aceleración centrípeta (incluso si se mueve con velocidad constante). Pero en el caso de cambio de velocidad, actuará una aceleración tangencial en el sentido o en el contrario de la dirección de la velocidad.
Por ejemplo, si un coche acelera en una trayectoria curva en la carretera, entonces experimenta tanto la aceleración tangencial como la centrípeta. ¿Sabes qué es la aceleración tangencial en un movimiento circular y cómo funciona? En este artículo, encontraremos la expresión de la aceleración tangencial.
Fórmula de aceleración tangencial
En un movimiento circular uniforme, la fuerza neta que actúa sobre el objeto está en la dirección perpendicular al movimiento del objeto. Por lo tanto, esto provoca un cambio en la dirección continuamente, pero la magnitud de la velocidad permanece constante. En consecuencia, se dice que el objeto se acelera en una dirección que apunta hacia el centro de la trayectoria circular. Pero, ¿qué ocurre cuando la fuerza neta que actúa sobre el objeto no es perpendicular? En este caso, habrá vectores de fuerza de dos componentes que apuntarán a la perpendicular y a la paralela al vector velocidad. La componente perpendicular de la fuerza hará que el objeto se mueva a lo largo de una trayectoria circular, ya que crea una aceleración centrípeta, y la componente paralela de la fuerza hará que el objeto se acelere a lo largo de la tangente, ya que crea una aceleración tangencial. Por lo tanto, el objeto experimentará un movimiento circular no uniforme, ya que tanto la dirección como la magnitud de la velocidad del objeto cambiarán.
Notaciones utilizadas en la fórmula
- at es la aceleración tangencial
- Δv es el cambio en la velocidad angular
- Δt es el cambio en el tiempo
- v es la velocidad lineal
- s es la distancia recorrida
- t es el tiempo empleado
La fórmula de la aceleración tangencial se utiliza para calcular la aceleración tangencial y los parámetros relacionados y la unidad es m/s2
Fórmula de la aceleración lineal
La aceleración lineal se define como la aceleración uniforme causada por un cuerpo en movimiento en una línea recta. Hay tres ecuaciones que son importantes en la aceleración lineal dependiendo de los parámetros como la velocidad inicial y final, el desplazamiento, el tiempo y la aceleración.
La siguiente tabla explica las tres ecuaciones que se utilizan en la aceleración lineal:

Notaciones utilizadas en la fórmula
- u es la velocidad inicial
- a es la aceleración
- t es el tiempo empleado
- v es la velocidad final
- s es la aceleración
Ejemplo resuelto de Aceleración tangencial
Con una velocidad de 20 m/s a 80 m/s en 30s, un cuerpo acelera uniformemente sobre una trayectoria circular. Calcular la aceleración a la tangencial.
Solución:
Dados los parámetros
vi = 20 m/s
vf = 80 m/s
dv = vf - vi = 80 - 20 = 60 m/s
dt = tf - ti = 30 - 0 = 30seg.
La fórmula de la aceleración tangencial es
at = dv / dt
at = 60 / 30
at = 2 m/s2
Vídeos de Aceleración tangencial