Ángulo entre dos rectas
Siempre que dos rectas se cruzan, forman dos conjuntos de ángulos. La intersección forma un par de ángulos agudos y otro par de ángulos obtusos. Los valores absolutos de los ángulos formados dependen de las pendientes de las rectas que se cruzan.
También cabe destacar aquí que el ángulo formado por la intersección de dos rectas no se puede calcular si una de las rectas es paralela al eje y, ya que la pendiente de una recta paralela al eje y es una indeterminada.
Fórmula del ángulo entre dos rectas
Si θ es el ángulo entre dos rectas que se cruzan definidas por y1= m1x1+c1 e y2= m2x2+c2, entonces, el ángulo θ viene dado por
tanθ=±(m2-m1) / (1+m1m2)
Derivación del ángulo entre dos rectas
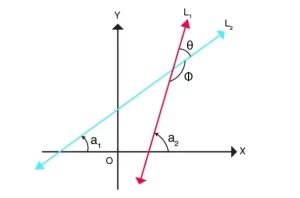
Considera el siguiente diagrama:
En el diagrama anterior, la recta L1 y la recta L2 se cruzan en un punto.
La medida de la pendiente se puede tomar como
tan a1 = m1 y tan a2 = m2
Además, de la figura, podemos deducir que θ = a2-a1
Ahora, tan θ = tan (a2-a1) = (tan a2 - tan a1 ) / (1- tan a1tan a2)
Sustituyendo los valores de tan a1 y tan a2 por m1 y m2 respectivamente, tenemos
tanθ= (m2 - m1 ) / (1+m1m2)
Hay que tener en cuenta que el valor de tan θ en esta ecuación será positivo si θ es agudo y negativo si θ es obtuso.
Ángulo entre dos líneas Geometría de coordenadas
En geometría analítica, si se dan las coordenadas de tres puntos A, B y C, el ángulo entre las rectas AB y BC se puede calcular de la siguiente manera:
Para una recta cuyos puntos extremos son (x1, y1) y (x2, y2), la pendiente de la recta viene dada por la ecuación
m = y2-y1/x2-x1
El ángulo entre las dos rectas se puede hallar calculando la pendiente de cada una de ellas y utilizándolas después en la fórmula para determinar el ángulo entre dos rectas cuando se conoce la pendiente de cada una de ellas a partir de la ecuación
tan θ=± (m1 - m2 ) / (1+ m1m2)
En la siguiente sección exploraremos los problemas numéricos con solución.
Problema con solución
Si P (-2, 1), Q (2, 3) y R (-2, -4) son tres puntos, encuentra el ángulo entre las rectas PQ y QR.
La pendiente de PQ viene dada por
m = ( y2 - y1 ) / (x2 - x1)
m =( 3 - 1 ) / (2 - (-2 ))
m= 2/4
Por lo tanto, m1=1/2
La pendiente de la QR viene dada por
m= (-4-3) / (-2-2)
m= 7/4
Por lo tanto, m2 = 7/4
Sustituyendo los valores de m2 y m1 en la fórmula del ángulo entre dos rectas cuando conocemos las pendientes de dos lados, tenemos
tan θ=± (m2 - m1 ) / (1+m1m2)
tan θ=± ((7/4) - (1/2) ) / (1+ (1/2)(7/4))
tan θ=± (2/3)
Por lo tanto, θ = tan -1 (⅔)
Vídeos de Ángulo entre dos rectas
Entradas Relacionadas
Contenido