Asintotas de la hiperbola

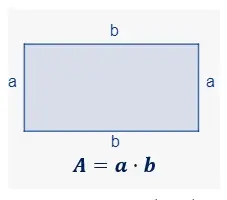
Las hipérbolas resultan cuando un plano y un cono doble derecho se intersecan y cubren las intersecciones superior e inferior, como se muestra a continuación. Esto significa que las hipérbolas son dos curvas en forma de U (llamadas ramas) que se enfrentan entre sí. Pueden estar orientadas verticalmente, como en nuestro ejemplo, u orientadas horizontalmente.

• La imagen de arriba nos muestra los diferentes componentes de una hipérbola independientemente de su orientación.
• Las hipérbolas tienen dos curvas llamadas ramas que se enfrentan entre sí.
• Al tener dos curvas en forma de U, las hipérbolas también tendrán dos vértices y focos.
• El eje transversal es un eje director que divide la hipérbola por la mitad.

Las hipérbolas constan de dos piezas que tienen una forma similar a las parábolas. Una pieza se abre hacia arriba y la otra hacia abajo o una hacia la izquierda y la otra hacia la derecha. También, de forma similar a las parábolas, cada una de las piezas tiene un vértice. Las gráficas de las hipérbolas también tienen dos líneas, que se llaman asíntotas. Las asíntotas no forman parte oficialmente de las hipérbolas, pero se incluyen para asegurarnos de que obtenemos la gráfica correcta. Los elementos más importantes de una hipérbola son los focos, los vértices, los ejes, la distancia focal, los semiejes y las asíntotas.

Elementos fundamentales de una hipérbola

Los siguientes son los elementos fundamentales de una hipérbola:

• Focos
• Eje transversal
• Eje conjugado
• Eje semimayor
• Eje semimayor
• Centro
• Vértices
• Longitud focal
• Ejes de simetría
• Asíntotas

Asíntotas

Las asíntotas son las líneas que están muy cerca de las ramas de la hipérbola pero que nunca la tocan. Las asíntotas se cruzan en el centro de la hipérbola.

Definición y forma estándar

Una hipérbola puede abrirse hacia la izquierda y hacia la derecha o abrirse hacia arriba y hacia abajo. Una definición más formal de una hipérbola es un conjunto de todos los puntos, cuyas distancias a dos puntos fijos, llamados focos, es una diferencia constante. La ecuación de una hipérbola en forma estándar es

((x - h)^2 / a^2) - ((y - k)^2 / b^2) = 1

La x y la y son intercambiables y ambas te dan la ecuación de una hipérbola. Veamos algunas de sus partes.

Partes de una hipérbola

Centro
Observa que la hipérbola tiene dos líneas de simetría: una vertical y otra horizontal. Puedes doblar la hipérbola para que una mitad quede completamente encima de la otra. Los pliegues crearán dos líneas. El punto en el que se cruzan el pliegue vertical y el horizontal se llama centro de la hipérbola. Utilizando la forma estándar de la hipérbola, el centro se encuentra en el punto (h, k).

Vértices

El vértice de una parábola es el punto más bajo de una parábola si se abre hacia arriba y el punto más alto si se abre hacia abajo. Los vértices de una hipérbola (que está compuesta por dos parábolas) es el vértice de cada rama de la hipérbola. Para utilizar la forma estándar de la hipérbola para encontrar los vértices, tienes que fijarte en si el término positivo es x^2 o y^2. Si el término positivo es x^2, los vértices se encuentran en (h + a, k) y (h - a, k). Si y^2 es el primer término, los vértices se encuentran en (h, k + b) y (h, k - b).

Asíntotas

Las asíntotas de una hipérbola son dos líneas que se encuentran entre las dos ramas de la hipérbola. La intersección de las dos líneas se produce en el centro de la hipérbola. Las rectas se acercan a la hipérbola pero no la cruzan. Si la ecuación tiene un término x^2 positivo, las ecuaciones de las rectas serán

(y - k) = +b/a(x - h)
(y - k) = -b/a(x - h)

Si el término y^2 es positivo, las ecuaciones serán las mismas, excepto que b/a se sustituye por a/b.

Vídeos de Asintotas de la hiperbola