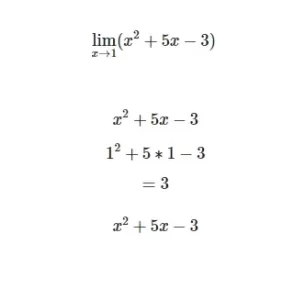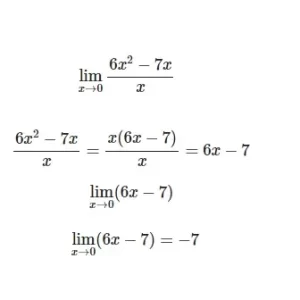Cálculo de límites

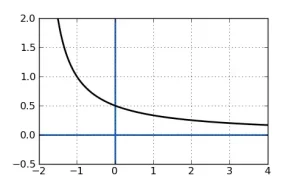
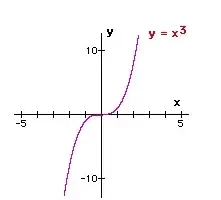
Por ejemplo, el límite de la siguiente gráfica es 0 a medida que x se acerca al infinito, lo que se ve claramente cuando la gráfica se acerca a 0 de esta manera:

Veamos ahora algunos ejemplos en los que podemos encontrar el límite de funciones reales:

Ejemplo A

Encuentra el límite de

f(x)=4x, a medida que x se acerca a 3.

Pasos:

1) Sustituir x por 3.
2) Simplificar.

f(x)=4x se convierte en f(3)=4(3)=12

Por tanto, el límite de:

f(x)=4x a medida que x se acerca a 3 es 12.

En este caso, la solución es sencilla, porque la función no sólo se acerca a 12, sino que pasa por él.

Ejemplo B

Encuentra el límite:

lim x → 1(x2+5x-3)

Sigue los mismos pasos que en el caso anterior.

a medida que x se acerca a 1 es 3.

Sin embargo, el método de sustitución no siempre funciona. Para el Ejemplo C a continuación, debes factorizar el numerador primero ANTES de aplicar el método de sustitución.

Ejemplo C

Si sustituimos 0 por x en el ejemplo C, crearemos una división por cero que NO EXISTE o es INDEFINIDA. Esa es la razón por la que la factorización DEBE ser nuestro primer paso en este ejemplo. Tenemos que limpiarlo un poco para que no haya división por cero.

Factorizando el numerador de x, que es común a ambos términos

Anulamos un factor de x en el numerador y el denominador, lo que nos deja un límite simple:

Ahora, podemos sustituir x por 0 para encontrar que el límite es -7:

Nota: Aunque hayamos podido simplificar la función en la muestra C mediante la factorización, no podemos pretender que no haya ocurrido. Recuerda que estábamos encontrando el límite a medida que x se acercaba a 0, no tratando de evaluar la función EN x=0. La función sigue siendo indefinida en x=0. Sin embargo, tiene un límite. Sólo la versión simplificada tiene una solución en x=0. Sólo después de la factorización, en algunos casos, podemos aplicar la sustitución para encontrar el límite.

Vídeos de Cálculo de límites

https://www.youtube.com/watch?v=uVwa7hHiROc