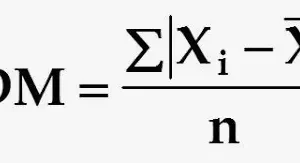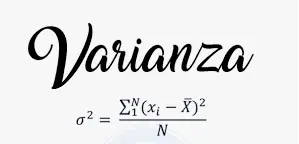Coeficiente de asimetría fórmula
- Las distribuciones pueden presentar una asimetría a la derecha (positiva) o a la izquierda (negativa) en distintos grados.
- Una distribución normal (curva de campana) presenta una asimetría nula.
- Los inversores se fijan en la asimetría derecha cuando juzgan una distribución de rentabilidad porque, al igual que el exceso de curtosis, representa mejor los extremos del conjunto de datos en lugar de centrarse únicamente en la media.
Entender la asimetría
Además de la asimetría positiva y negativa, también se puede decir que las distribuciones tienen asimetría cero o indefinida. En la curva de una distribución, los datos del lado derecho de la curva pueden estrecharse de forma diferente a los datos del lado izquierdo. Estos estrechamientos se conocen como "colas". El sesgo negativo se refiere a una cola más larga o más gorda en el lado izquierdo de la distribución, mientras que el sesgo positivo se refiere a una cola más larga o más gorda en la derecha.
La media de los datos sesgados positivamente será mayor que la mediana. En una distribución sesgada negativamente, ocurre exactamente lo contrario: la media de los datos sesgados negativamente será menor que la mediana. Si los datos se grafican de forma simétrica, la distribución tiene cero asimetría, independientemente de lo largas o gordas que sean las colas.
Las tres distribuciones de probabilidad representadas a continuación tienen un grado creciente de asimetría positiva (o asimetría derecha). Las distribuciones con sesgo negativo también se conocen como distribuciones con sesgo izquierdo.
La asimetría se utiliza junto con la curtosis para juzgar mejor la probabilidad de que los eventos caigan en las colas de una distribución de probabilidad.
Medición de la asimetría
Hay varias formas de medir la asimetría. El primer y el segundo coeficiente de asimetría de Pearson son dos de los más comunes. El primer coeficiente de asimetría de Pearson, o asimetría modal de Pearson, resta la moda de la media y divide la diferencia por la desviación estándar. El segundo coeficiente de asimetría de Pearson, o asimetría de la mediana de Pearson, resta la mediana de la media, multiplica la diferencia por tres y divide el producto por la desviación estándar.
¿Qué le dice la asimetría?
Los inversores se fijan en la asimetría a la hora de juzgar una distribución de rentabilidad porque, al igual que la curtosis, tiene en cuenta los extremos del conjunto de datos en lugar de centrarse únicamente en la media. Los inversores a corto y medio plazo, en particular, necesitan fijarse en los extremos porque es menos probable que mantengan una posición el tiempo suficiente para confiar en que la media se resuelva por sí sola.
Los inversores suelen utilizar la desviación estándar para predecir los rendimientos futuros, pero la desviación estándar supone una distribución normal. Como pocas distribuciones de rentabilidad se acercan a la normalidad, la asimetría es una medida mejor para basar las predicciones de rentabilidad. Esto se debe al riesgo de asimetría.
El riesgo de asimetría es el mayor riesgo de que aparezca un punto de datos de alta asimetría en una distribución asimétrica. Muchos modelos financieros que intentan predecir el rendimiento futuro de un activo asumen una distribución normal, en la que las medidas de tendencia central son iguales. Si los datos son asimétricos, este tipo de modelo siempre subestimará el riesgo de asimetría en sus predicciones. Cuanto más sesgados estén los datos, menos preciso será este modelo financiero.
Vídeos de Coeficiente de asimetría fórmula
Entradas Relacionadas
Contenido