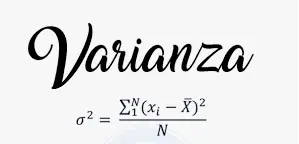Coeficiente de variación interpretación
El coeficiente de variación (CV) es una medida relativa de la variabilidad que indica el tamaño de una desviación estándar en relación con su media. Es una medida estandarizada y sin unidades que permite comparar la variabilidad entre grupos y características dispares. También se conoce como desviación estándar relativa (RSD).
En este post, aprenderá sobre el coeficiente de variación, cómo calcularlo, saber cuándo es especialmente útil y cuándo hay que evitarlo.
Cómo calcular el coeficiente de variación
El cálculo del coeficiente de variación consiste en una simple relación. Basta con tomar la desviación estándar y dividirla por la media.
Ecuación del coeficiente de variación
Los valores más altos indican que la desviación estándar es relativamente grande en comparación con la media.
Por ejemplo, una pizzería mide su tiempo de entrega en minutos. La media del tiempo de entrega es de 20 minutos y la desviación estándar es de 5 minutos.
Interpretación del coeficiente de variación
Para el ejemplo del reparto de pizza, el coeficiente de variación es 0,25. Este valor indica el tamaño relativo de la desviación estándar en comparación con la media. Los analistas suelen informar del coeficiente de variación en forma de porcentaje. En este ejemplo, la desviación estándar es el 25% del tamaño de la media.
Si el valor es igual a uno o al 100%, la desviación estándar es igual a la media. Los valores inferiores a uno indican que la desviación típica es menor que la media (típica), mientras que los valores superiores a uno se producen cuando la D.S. es mayor que la media.
En general, los valores más altos representan un mayor grado de variabilidad relativa.
Medidas de variabilidad absolutas y relativas
En el caso de la desviación estándar de cinco minutos en el ejemplo de la entrega de pizzas, sabemos que la entrega típica se produce cinco minutos antes o después del tiempo medio de entrega.
Esta información es muy útil. Nos indica la variabilidad de nuestros datos utilizando, convenientemente, las unidades de medida originales. Podemos comparar esta variabilidad del tiempo de entrega con otra pizzería.
Por otro lado, las medidas relativas utilizan un proceso de estandarización que elimina las unidades de medida originales. En el coeficiente de CV, tanto la desviación estándar como la media utilizan las mismas unidades, lo que las anula y produce una estadística sin unidades.
¿Cuándo querrá utilizar el coeficiente de variación? Su naturaleza sin unidades le proporciona algunas ventajas. En concreto, el coeficiente de variación facilita las comparaciones significativas en escenarios en los que las medidas absolutas no pueden.
Utilice el coeficiente de variación cuando quiera comparar la variabilidad entre:
- Grupos que tienen medias de magnitudes muy diferentes.
- Características que utilizan diferentes unidades de medida.