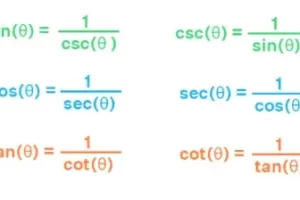Derivada seno

La derivada de sen x con respecto a x es cos x. Se representa como d/dx(sen x) = cos x (o) (sen x)' = cos x. Es decir, la derivada de la función seno de una variable con respecto a la misma variable es la función coseno de la misma variable,

d/dy (sen y) = cos y
d/dθ (sin θ) = cos θ

Fórmula de la derivada de sen x

La derivada de sen x es cos x. Vamos a demostrarlo en cada uno de los siguientes métodos.

Por primer principio
Por la regla de la cadena
Por la regla del cociente

Derivada de Sin x Prueba por primer principio

La definición de límite de la derivada (primer principio) se utiliza para encontrar la derivada de cualquier función. Vamos a utilizar el primer principio para encontrar también la derivada de sen x. Para ello, supongamos que f(x) = sen x es la función a diferenciar. Entonces f(x + h) = sin(x + h). Ahora, por el primer principio, la definición de límite de la derivada de una función f(x) es

f'(x) = limₕ→₀ [f(x + h) - f(x)] / h

Sustituyendo aquí f(x) = sen x y f(x + h) = sen(x + h)

f'(x) = limₕ→₀ [sin(x + h) - sin x] / h

Podemos evaluar este límite por dos métodos.

Método 1

Por una de las fórmulas trigonométricas, sin C - sin D = 2 cos [(C + D)/2] sin [(C - D)/2]. Aplicando esto

f'(x) = limₕ→₀ [2 cos[(x + h + x)/2] sin[(x + h - x)/2] ] / h

= limₕ→₀ [2 cos[(2x + h)/2] sin (h/2) ] / h

= limₕ→₀ [cos[(2x + h)/2] - limₕ→₀ [sin (h/2) ] / (h/2)]

Como h → 0, (h/2) → 0. Por tanto

f'(x) = limₕ→₀ [cos[(2x + h + x)/2] - lim₍ₕ/₂₎→₀ [sin (h/2) ] / (h/2)]

Utilizando fórmulas de límite, lim ₓ→₀ (sin x/x) = 1. Así que

f'(x) = [cos[(2x + 0)/2] - (1) = cos (2x/2) = cos x

Así, hemos demostrado que la derivada de sen x es cos x.

Método 2

Por fórmulas de suma y diferencia,

sin (A + B) = sin A cos B + cos A sin B

Usando esto

f'(x) = limₕ→₀ [sen x cos h + cos x sen h - sen x] / h

= limₕ→₀ [ - sin x (1- cos h) + cos x sin h] / h

= limₕ→₀ [ - sin x (1 - cos h)]/h + limₕ→₀ (cos x sin h)/h

= -sin x limₕ→₀ (1 - cos h)/h + (cos x) limₕ→₀ sin h/h

Utilizando las fórmulas de medio ángulo, 1 - cos h = 2 sin2(h/2).

f'(x) = -sin x limₕ→₀ (2 sin2(h/2))/h + (cos x) limₕ→₀ sin h/h

= -sin x [limₕ→₀ (sin(h/2))/(h/2) - limₕ→₀ sin (h/2)] + (cos x) (limₕ→₀ sin h/h)

Sabemos que lim ₓ→₀ (sen x/x) = 1.

f'(x) = -sin x (1 - sin(0/2)) + cos x (1)

= -sin x(0) + cos x (De la tabla trigonométrica, sin 0 = 0)

= cos x

Por tanto, hemos deducido que la derivada de sen x es cos x.

Derivada de Sin x Prueba por la regla de la cadena

Por la regla de la cadena de la diferenciación, d/dx(f(g(x)) f'(g(x)) - g'(x). Así que para encontrar la derivada de sen x usando la regla de la cadena, debemos escribirla como una función compuesta. Utilizando una de las fórmulas trigonométricas, podemos escribir sen x como, sen x = cos (π/2 - x). Usando esto podemos encontrar la derivada de y = sin x (o) cos (π/2 - x).

Usando la regla de la cadena,

y' = - sin(π/2 - x) - d/dx (π/2 - x) (ya que la derivada de cos x es - sin x)

= - sin(π/2 - x) - (-1)

= sin(π/2 - x)

= cos x (Por una de las fórmulas trigonométricas).

Así, hemos derivado la fórmula de la derivada de sen x por la regla de la cadena.

Prueba de la derivada de sen x por la regla del cociente

La regla del cociente dice que d/dx (u/v) = (v u' - u v') / v2. Así que para encontrar la diferenciación de sen x usando la regla del cociente, tenemos que escribir sen x como una fracción. Sabemos que sin es el recíproco de la función cosecante (csc). es decir, y = sin x = 1/(csc x). Entonces, por la regla de la cadena

y' = [csc x - d/dx(1) - 1 - d/dx(csc x)] / csc2x

= [csc x (0) - 1 (-csc x cot x)] / csc2x (ya que la derivada de csc x es -csc x cot x]

= (cot x) / (csc x)

= [(cos x)/(sin x)] / [1/sin x]

= cos x

Por tanto, la derivada de sin es cos x y se demuestra utilizando la regla del cociente.

Derivada de la función compuesta Sin(u(x))

sin(u(x)) es una función compuesta y por lo tanto se puede escribir como sin(u(x)) = f(g(x)) donde g(x) = u(x) y f(x) = sen x. Entonces g'(x) = u'(x) y f'(x) = cos x. Sabemos que la derivada de una función compuesta se encuentra utilizando la regla de la cadena. Utilizando la regla de la cadena

d/dx (sin(u(x)) = f'(g(x)) - g'(x)

Como f'(x) = cos x y g(x) = u(x), tenemos f'(g(x)) = cos (u(x)). Así que

d/dx (sin(u(x)) = cos (u(x)) - u'(x)

Por tanto, la derivada de la función compuesta sin(u(x)) es cos (u(x)) - u'(x).

Notas importantes sobre la derivada de Sin x:

Aquí hay algunos puntos importantes a tener en cuenta de la diferenciación de sen x.

• La derivada de sen x con respecto a x es cos x.
• La derivada de sen u con respecto a x es, cos u - du/dx.
• Sin x es máximo en x = π/2, 5π/2, .... y mínimo en x = 3π/2, 7π/2, ...
• En todos estos puntos, la derivada de sen x es 0. es decir, en todos estos puntos cos x = 0.
• La derivada de cos x NO es sin x, sino que es -sin x.

Vídeos de Derivada seno