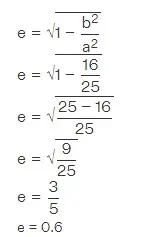Excentricidad de la elipse
Los dos términos importantes a los que debemos referirnos antes de hablar de la excentricidad son el foco y la directriz de la elipse. Para una sección cónica, el lugar de un punto cualquiera de la misma es tal que su relación entre la distancia al punto fijo -foco- y su distancia a la línea fija -directriz- es un valor constante que se denomina excentricidad.
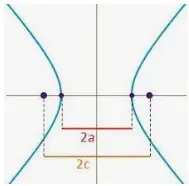
Excentricidad: (e < 1). Es la relación entre la distancia del foco al centro de la elipse y la distancia de un extremo de la elipse al centro de la misma. Si la distancia del foco al centro de la elipse es 'c' y la distancia del extremo de la elipse al centro es 'a', entonces la excentricidad e = c/a.
Fórmula de la excentricidad de la elipse
La excentricidad de una elipse es siempre menor que 1. Es decir, e < 1. La excentricidad de una elipse puede tomarse como el cociente entre su distancia al foco y la distancia a la directriz.
Excentricidad = Distancia al Foco/Distancia a la Directriz
Excentricidad de la elipse
e = c/a
Sustituyendo el valor de c tenemos el siguiente valor de excentricidad.
Aquí a es la longitud del semieje mayor y b es la longitud del semieje menor.
Derivación de la excentricidad de la elipse
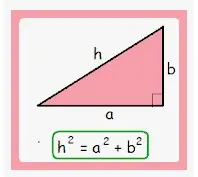
El primer paso en el proceso de derivar la ecuación de la elipse es derivar la relación entre el semieje mayor, el semieje menor y la distancia del foco al centro. El objetivo es encontrar la relación entre a, b, c. La longitud del eje mayor de la elipse es 2a y la longitud del eje menor de la elipse es 2b. La distancia entre los focos es igual a 2c. Tomemos un punto P en uno de los extremos del eje mayor y busquemos la suma de las distancias de este punto a cada uno de los focos F y F'.
PF + PF' = OP - OF + OF' + OP
= a - c + c + a
PF + PF'= 2a
Ejemplo de Excentricidad de la elipse
Encuentra la excentricidad de la elipse que tiene la ecuación x2/25 + y2/16 = 1.
Solución:
La ecuación dada de la elipse es x2/25 + y2/16 = 1. Comparando esto con la ecuación de la elipse x2/a2 + y2/b2 = 1, tenemos que a2 = 25, y b2 = 16.
La fórmula de la excentricidad de una elipse es la siguiente
Respuesta: Por tanto, la excentricidad de la elipse es 0,6.
Vídeos de Excentricidad de la elipse
Entradas Relacionadas
Contenido