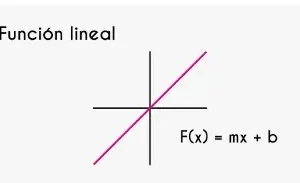
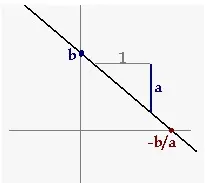
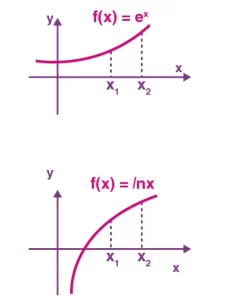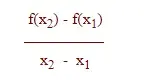Función decreciente

En ambas funciones dadas x1 < x2 y F(x1) < F(x2), por lo que podemos decir que es una función creciente.

F(x) = e-x

Funciones crecientes y decrecientes

Todos sabemos que si algo es creciente es que está subiendo y si es decreciente es que está bajando. Otra forma de decir que una gráfica está subiendo es que su pendiente es positiva. Si la gráfica está bajando, la pendiente será negativa. Como pendiente y derivada son sinónimos, podemos relacionar el aumento y la disminución con la derivada de una función. Primero una definición formal.

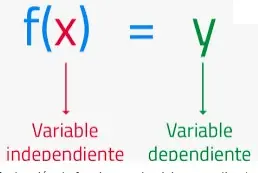
Una función es creciente en un intervalo si para cualquier x1 y x2 en el intervalo entonces

x1 < x2 implica f(x1) < f(x2)

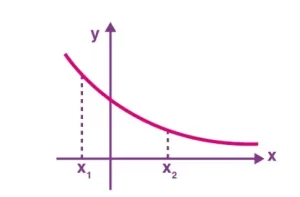
Una función es decreciente en un intervalo si para cualquier x1 y x2 en el intervalo entonces

x1 < x2 implica f(x1) > f(x2)

¿Cómo se relaciona esto con las derivadas? Recuerda que la derivada es el límite

Si x1 < x2, entonces el denominador será positivo. Si también f(x1) < f(x2), entonces el numerador será positivo, por lo que la derivada será positiva. Por otro lado si f(x1) > f(x2), entonces el numerador será negativo y la derivada será negativa. esto nos lleva al siguiente teorema.

Teorema sobre las derivadas y las funciones crecientes/decrecientes

Sea f una función diferenciable en el intervalo (a,b), entonces

Si f '(x) < 0 para x en (a,b), entonces f es decreciente allí.
Si f '(x) > 0 para x en (a,b), entonces f es creciente allí.
Si f '(x) = 0 para x en (a,b), entonces f es constante.

Ejemplos y números críticos

Determina los valores de x donde la función

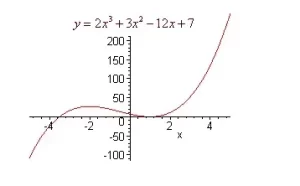
f(x) = 2x3 + 3x2 - 12x + 7

Solución

Primero tomamos la derivada

f '(x) = 6x2 + 6x - 12

Para determinar dónde la derivada es positiva y dónde es negativa, encuentra las raíces. Factorizamos para obtener

6(x2 + x - 2) = 6(x - 1)(x + 2)

Por tanto, el cambio de signo puede producirse cuando

x = 1 y x = -2

Ahora crea algunos valores de prueba

La derivada es positiva fuera de [-2,1] y es negativa dentro de [-2,1]. Podemos concluir que f es creciente fuera de [-2,1] y decreciente dentro de [-2,1]. La gráfica se muestra a continuación.

Vimos que los valores de x tales que la derivada es 0 eran de especial interés. Otros puntos en los que podría haber un cambio de creciente a decreciente es cuando la derivada es indefinida.

Llamamos a c un número crítico si f '(c) = 0 o f '(c) es indefinido.

Vídeos de Función decreciente