Analisis

Función identidad

Funcion identidad
Sea R el conjunto de los números reales. Así, la función de valor real f : R → R por y = f(a) = a para todo a ∈ R, se llama función de identidad. Aquí el dominio y el rango (codominio) de la función f son R. Por tanto, cada elemento del conjunto R tiene una imagen sobre sí mismo. La gráfica es una recta y pasa por el origen. La aplicación de esta función puede verse en la matriz identidad. Matemáticamente se puede expresar como f(a) = a ∀ a ∈ R Donde a es el elemento del conjunto R. Por ejemplo, f(2) = 2 es una función identidad. En la teoría de conjuntos, cuando una función se describe como un tipo particular de relación binaria, la función de identidad viene dada por la relación de identidad o diagonal de A, donde A es un conjunto.

Función identidad

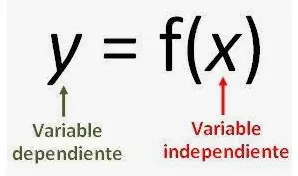
Una función en matemáticas es una relación binaria entre dos conjuntos. Cada elemento del primer conjunto tiene un único representante en el otro conjunto. Toda función matemática que conserva el valor de la variable incluso después de realizar la operación indicada en la función se llama función de identidad. Una función de identidad también se llama relación de identidad o transformación de identidad o mapa de identidad. Una función identidad siempre devuelve el mismo valor que se utiliza como argumento. Una función de identidad se representa en general como:

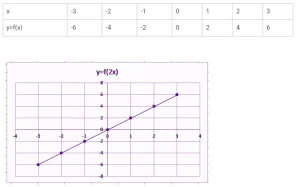
Demuestra que f(2x) = 2x es una función identidad.

Solución: Dada, f(2x) = 2x

Pongamos los valores de x en la función dada.

Si x = 1, entonces

f(2(1)) = 2(1) ⇒ f(2) = 2

Si x = 2, entonces

f(2(2)) = 2(2) ⇒ f(4) = 4

Leer  Funcion a trozos

Si x = 3, entonces

f(2(3)) = 2(3) ⇒ f(6) = 6

Si x = 0, entonces

f(2(0)) = 2(0) ⇒ f(0) = 0

Probemos con algunos valores negativos de x.

Si x =-1, entonces;

f(2(-1)) = 2(-1) ⇒ f(-2) = -2

Si x = -2, entonces

f(2(-2)) = 2(-2) ⇒ f(-4) = -4

Si x = -3, entonces;

f(2(-3)) = 2(-3) ⇒ f(-6) = -6

Dibujemos una tabla para todos los valores de x.

Propiedades de la función de identidad

  • Es un operador lineal en caso de aplicación de espacios vectoriales.
  • Para números enteros positivos, es una función multiplicativa.
  • Para un espacio vectorial m-dimensional, se expresa como matriz de identidad Im.
  • En el espacio topológico, esta función es siempre continua.

Vídeos de Función identidad

Entradas Relacionadas

Ley de hooke
Cálculo de límites
Polígono de frecuencia

Contenido

Entradas Relacionadas