Funciones inyectivas

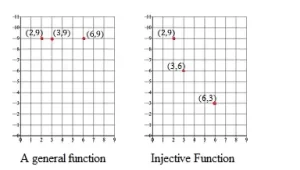
No es necesario que todos los puntos posibles de la función (el "codominio") estén mapeados. Pero los que lo están deben asignar una entrada distinta a una salida distinta.

Identificación de funciones inyectivas

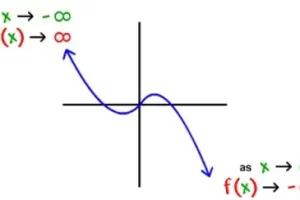
Puedes averiguar si una función es inyectiva representándola gráficamente. Una función inyectiva debe ser continuamente creciente o continuamente decreciente. Busca zonas en las que la función cruce una línea horizontal en al menos dos lugares; si esto ocurre, la función cambia de dirección (por ejemplo, de creciente a decreciente), por lo que no es inyectiva.

Algunas reglas rápidas para identificar las funciones inyectivas:

• Si una función está definida por una potencia impar, es inyectiva. La función lineal simple f(x) = 2 x + 1 es inyectiva en ℝ (el conjunto de todos los números reales), porque cada x distinta nos da una respuesta distinta f(x).
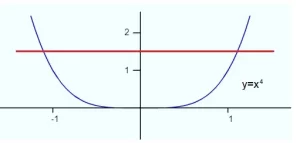
• Si una función está definida por una potencia par, no es inyectiva. Un ejemplo es la función x4, que no es inyectiva en todo su dominio (el conjunto de todos los números reales). El valor de la función en x = 1 es igual al valor de la función en x = 1. Sin embargo, si se restringe el dominio a un lado del eje y, entonces la función es inyectiva. Por ejemplo, si el dominio se define como reales no negativos, [0,+∞).

Notación y definición formal

A veces las funciones que son inyectivas se designan con una flecha con una cola de púas que va entre el dominio y el rango, así f: X ↣ Y.

Supongamos que f es una función sobre el dominio X. Que f sea inyectiva significa que para todo a y b en X, si f(a) = f(b), a = b. Si a y b no son iguales, entonces f(a) ≠ f(b).

Podemos escribir esto en símbolos matemáticos diciendo

que leemos como "para todo a, b en X, que f(a) sea igual a f(b) implica que a es igual a b".

Las funciones pueden ser inyecciones (funciones uno a uno), suryecciones (funciones sobre) o biyecciones (tanto uno a uno como sobre). Informalmente, una inyección tiene cada salida asignada a un máximo de una entrada, una suryección incluye todo el rango posible en la salida, y una biyección tiene ambas condiciones verdaderas.

Vídeos de Funciones inyectivas

https://www.youtube.com/watch?v=slaiEUcAa60