Intervalos de crecimiento y decrecimiento

Una derivada es un punto de la función que nos da la medida de la tasa de cambio de la función en ese punto concreto. Geométricamente hablando, nos dan información sobre la pendiente de la tangente en ese punto. Esta información puede utilizarse para averiguar los intervalos o las regiones en las que la función es creciente o decreciente. Una vez conocidos dichos intervalos, no es muy difícil averiguar los valles y colinas de la gráfica de la función. La figura siguiente muestra una función f(x) y sus intervalos en los que aumenta y disminuye.

Para una función f(x). Para un intervalo I definido en su dominio.

Se dice que la función f(x) es creciente en un intervalo I si para todo a < b, f(a) ≤ f(b).
La función f(x) se dice decreciente en un intervalo I si para todo a < b, f(a) ≥ f(b).
La función se llama estrictamente creciente si para cada a < b, f(a) < f(b). Una definición similar es válida para el caso estrictamente decreciente.

Intervalos crecientes y decrecientes

El objetivo es identificar estas zonas sin mirar la gráfica de la función. Para ello, vamos a mirar las derivadas de la función en estas regiones. El hecho de que estas derivadas no son más que la pendiente de las tangentes en esta curva ya está establecido. La figura siguiente muestra las pendientes de las tangentes en diferentes puntos de esta curva.

Observa que en las regiones donde la función es decreciente la pendiente de la curva es realmente negativa y positiva para las regiones donde la función es creciente. La pendiente en los picos y valles es cero. Así que, para decirlo formalmente

Digamos que f(x) es una función continua en [a, b] y diferenciable en el intervalo (a, b).

• Si f'(c) > 0 para todo c en (a, b), entonces se dice que f(x) es creciente en el intervalo.
• Si f'(c) < 0 para todo c en (a, b), se dice que f(x) es decreciente en el intervalo.
• Si f'(c) = 0 para todo c en (a, b), entonces se dice que f(x) es constante en el intervalo.

Puntos críticos

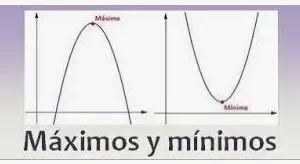
En el diagrama anterior observa cómo cuando la función pasa de decreciente a creciente o de creciente a decreciente. Se produce un valle o un pico. Estos valles y picos son puntos extremos de la función, por lo que se llaman extremos. En la figura es bastante evidente que en estos puntos la derivada de la función se hace cero. La función alcanza sus valores mínimos y máximos en estos puntos.

Nota: Una función puede tener cualquier número de puntos críticos. Aunque todos los puntos críticos no necesariamente dan el valor máximo y mínimo de la función. Pero cada punto crítico es un valle que es un punto mínimo en la región local.

En la figura anterior, hay tres extremos, dos de ellos son mínimos, pero sólo hay un máximo y un mínimo global. Así que en términos formales,

Para una función f(x), un punto x = c es extremo si

f'(c) = 0

Identificación de intervalos crecientes y decrecientes

De las figuras anteriores se desprende que todo extremo de la función es un punto en el que su derivada cambia de signo. Es decir, la función pasa de creciente a decreciente o viceversa. Al buscar regiones en las que la función es creciente o decreciente, resulta esencial mirar alrededor de los extremos. Para cualquier función f(x) y un intervalo dado, hay que seguir los siguientes pasos para encontrar estos intervalos:

• Comprobar si la función es diferenciable y continua en el intervalo dado.
• Resolver la ecuación f'(x) = 0, las soluciones de esta ecuación nos dan los extremos.
• Para un punto extremo x = c, busca en la región cercana a ese punto y comprueba los signos de las derivadas para averiguar los intervalos en los que la función es creciente o decreciente.

Vídeos de Intervalos de crecimiento y decrecimiento