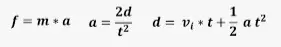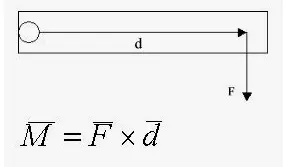Momento de un par de fuerzas

El momento de una fuerza que actúa en torno a un punto o eje se halla multiplicando la fuerza (F) por la distancia perpendicular al eje (d), llamada brazo de palanca.

Momento = Fuerza x Distancia perpendicular
M = F x d
(Nm) = (N) x (m)

Notas;
1. En el sentido de las agujas del reloj es un momento positivo.
2. Tenga cuidado con las unidades aquí - especialmente con los mm. Es mejor convertir todo a m primero.

Brazo de palanca perpendicular

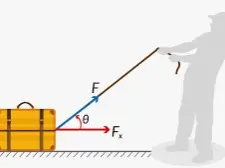
La fuerza no siempre es perpendicular al brazo de palanca dado. En este caso, hay que determinar la distancia perpendicular correcta. (Por cierto, la distancia perpendicular es también la distancia más corta entre la fuerza y el punto de giro).

Un momento puro no tiene fuerza, sólo rotación. El ejemplo siguiente muestra un soporte para contrarrestar la fuerza vertical de modo que sólo se aplique un momento puro (par) a la tuerca de la rueda.

Cuando se aplica un momento puro a un objeto, se puede mover a diferentes lugares sin cambiar nada - las reacciones son exactamente las mismas. Esto significa que el momento total puede calcularse en cualquier lugar del cuerpo y dar siempre la misma respuesta. Esto es muy práctico: podemos cualquier lugar (el más conveniente) para calcular el momento total.

El lugar más conveniente para tomar un momento suele ser la articulación más ocupada - como una articulación de pasador con múltiples fuerzas desconocidas (más sobre esto en el próximo capítulo).

Ejemplo: Destornillador en una ranura larga

El efecto de giro (par o momento) del destornillador es exactamente el mismo en todos los ejemplos anteriores. El momento aplicado es independiente de la ubicación del momento.

Momento vs. Par

En realidad no hay diferencia, ambos son efectos de giro y ambos se miden en Nm.

Una definición de libro de texto: Un efecto de giro se llama momento en situaciones estáticas (sin movimiento). En aplicaciones dinámicas (con movimiento), el efecto de giro se denomina par. Así, un eje de motor que gira tiene par, pero una palanca tiene momento. Esta es la definición de los libros de texto, pero en la práctica los dos términos se utilizan indistintamente. Por ejemplo, "llave de torsión".

Equilibrio de momentos

Cuando se trata de momentos, el equilibrio existe cuando el momento total es cero. (De lo contrario, se acelerará en la rotación, la aceleración angular). Matemáticamente, esto es muy sencillo: se suman los momentos en el sentido de las agujas del reloj y se restan los momentos en sentido contrario.
Para el equilibrio de los momentos;

"Tomando como positivo el sentido de las agujas del reloj, la suma de todos los momentos alrededor del punto A es cero"

Estos cálculos son muy sencillos. El error más común es no obtener la distancia perpendicular (más corta) entre el pivote y la fuerza. Otra cosa que hay que vigilar es no tener en cuenta los signos (momentos CW o CCW).

Acoplamiento de fuerzas

Dos fuerzas iguales de dirección opuesta, con una distancia d entre ellas causarán un momento, donde;
Un caso especial de momentos es un par. Un par consiste en dos fuerzas paralelas que son iguales en magnitud, opuestas en sentido y que no comparten una línea de acción. No produce ninguna traslación, sólo rotación. La fuerza resultante de un par es cero, pero produce un momento puro.

Una llave inglesa es un ejemplo de pareja. Las dos fuerzas de la mano son iguales pero de sentido contrario.
Tomando los momentos alrededor del centro (ambos en el sentido de las agujas del reloj);
Momento = F * d + F * d = 2Fd

El momento causado por un par = La fuerza * la distancia entre ellos.

Ejemplo de pareja: Abrazadera de rueda con dos manos empujando en direcciones opuestas.

Vídeos de Momento de un par de fuerzas