Perímetro de un triángulo isósceles

Donde,

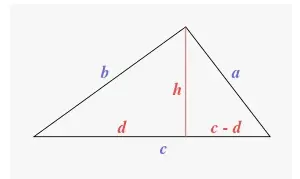
a = longitud de los dos lados iguales
b = Base del triángulo isósceles

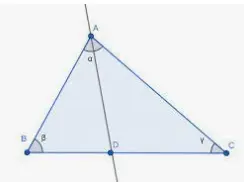
El perímetro de cualquier figura plana se define como la suma de las longitudes de los lados de la figura. Para un triángulo, el perímetro sería la suma de todos los lados del triángulo. Así, el perímetro un triángulo con longitudes de lado a, b y c, sería:

Perímetro de un triángulo = a + b + c unidades

En un triángulo rectángulo isósceles, sabemos que dos lados son congruentes. Supongamos que sus longitudes son iguales a l, y que la hipotenusa mide h unidades. Por tanto, el perímetro de un triángulo rectángulo isósceles sería

Perímetro = h + l + l unidades

Por tanto, el perímetro de un triángulo rectángulo isósceles P es h + 2l unidades.

Donde

h es la longitud del lado de la hipotenusa

l es la longitud de los lados adyacentes y opuestos

Ejemplo resuelto de perímetro de un triángulo isósceles

Pregunta 1: ¿Cuál es el perímetro de un triángulo isósceles cuando a = 9 cm y b = 6 cm?

Solución:

Dada,
a = 9 cm
b = 6 cm

Perímetro de un triángulo isósceles = 2a + b
= 2(9) + 6
= 18 + 6 cm
= 24 cm

Un triángulo rectángulo es un triángulo en el que exactamente un ángulo mide 90 grados. Como la suma de las medidas de los ángulos de un triángulo tiene que ser de 180 grados, es evidente que la suma de los dos ángulos restantes sería de otros 90 grados. Los dos lados perpendiculares se llaman los catetos de un triángulo rectángulo, y el lado más largo que se opone a los 90 grados se llama la hipotenusa de un triángulo rectángulo. Un triángulo rectángulo puede ser escaleno (con los tres lados de diferente longitud) o isósceles (con exactamente dos lados de igual longitud). Nunca puede ser un triángulo equilátero.

Definición de triángulo rectángulo isósceles

Un triángulo rectángulo isósceles es un triángulo rectángulo que consta de dos catetos de igual longitud. Como los dos catetos del triángulo rectángulo son de igual longitud, los ángulos correspondientes también son congruentes. Así, en un triángulo rectángulo isósceles, los dos catetos y los dos ángulos agudos son congruentes.

Triángulo rectángulo isósceles

Al tratarse de un triángulo rectángulo, el ángulo entre los dos catetos sería de 90 grados, y los catetos serían obviamente perpendiculares entre sí.

Fórmula del triángulo rectángulo isósceles

La fórmula más importante asociada a cualquier triángulo rectángulo es el teorema de Pitágoras. Según este teorema, el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los otros dos lados del triángulo rectángulo. Ahora bien, en un triángulo rectángulo isósceles, los otros dos lados son congruentes. Por tanto, tienen la misma longitud "l". Así, la hipotenusa mide h, entonces el teorema de Pitágoras para el triángulo rectángulo isósceles sería

(Hipotenusa)2 = (Lado)2 + (Lado)2

h2 = l2 + l2

h2 = 2l2

Además, dos ángulos congruentes en el triángulo rectángulo isósceles miden 45 grados cada uno, y el triángulo rectángulo isósceles es:

Área de un triángulo rectángulo, isósceles

Como sabemos que el área de un triángulo (A) es ½ bh unidades cuadradas

Donde

b es la base del triángulo

h es la altura del triángulo

En un triángulo rectángulo isósceles, dos catetos tienen la misma longitud. Digamos que ambos miden "l", entonces la fórmula del área puede modificarse a

Área, A = ½ (l × l)

A = ½ l2

Área de un triángulo rectángulo isósceles = l2/2 unidades cuadradas.

Donde

l es la longitud de los lados congruentes del triángulo rectángulo isósceles

Vídeos de Perímetro de un triángulo isósceles