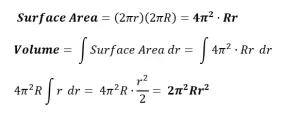Toro geometría

El círculo, que no tiene espesor, crea un tubo de diámetro y oquedad constantes. La existencia del Torus está limitada a una dimensión mínima de la tercera dimensión. Los toros de mayor dimensión se conocen como n-tor1 o hipertori.

Variaciones

Se pueden formar tres formas de tori en función del comportamiento del eje de revolución.

• Si el eje de revolución no tiene el círculo revolucionado que se interseca consigo mismo, se forma un toro normal.
• Si el eje de revolución tiene la intersección del círculo revuelto en un punto tangente, la superficie generada se convierte en un toro de cuerno. El cuerno se representa como un pico en el interior.
• Si el eje de revolución pasa dos veces por el círculo revuelto, se forma un toro de huso. El interior de los toros de huso contiene una geometría parecida a la de un huevo.

Tres tipos de toros: Normal (a), Cuerno (b) Huso (c)

Si el eje de revolución pasa por el centro del círculo girado, se generaría una esfera en lugar de un toroide.

Fundamentos geométricos

Para todos los tipos de toros, hay parámetros que son comunes en todos ellos y que hacen posible que existan sus representaciones gráficas. El radio desde el centro del toro hasta el centro del círculo que gira es el Radio Mayor, establecido como R. El radio del círculo en sí mismo se conoce como el Radio Menor, establecido como r.

Existen dos ángulos (θ, φ) donde θ representa el ángulo de rotación que toma el círculo giratorio (normalmente se toma una rotación completa, es decir, de 0 a 360 grados). El ángulo φ es el ángulo de inclinación del círculo revuelto, de manera que se puede hacer una curva más compleja.

Si se desconocen los ángulos, los toros pueden ser graficados usando ecuaciones implícitas en el Sistema de Coordenadas Cartesianas.

Los propios parámetros, tanto para los radios mayores como para los menores, se pueden encontrar desplazando términos de la función gráfica f(x, y, z) (Kriz, 2020).

Para los radios R y r, las relaciones entre ellos constituyen la base de la relación de aspecto (la relación del tamaño de la forma en diferentes dimensiones) y se relacionan con el tipo:

• R > r; la superficie revuelta se asemeja a los toros regulares.
• R = r; los círculos revueltos se cruzan consigo mismos en una tangente para formar toros de cuerno.
• R < r; la superficie revuelta se autointerseca para formar un toro de huso.

Ecuaciones de área y volumen de los toros

Si se visualizan los toros regulares como cilindros englobados, el área de es la de los cilindros de radio r y altura R:

Para el volumen de un toro, la integral del área de la superficie con respecto al radio r del círculo giratorio da como resultado la siguiente ecuación:

Aplicaciones en el mundo real

Existen numerosos productos fabricados por el hombre que se asemejan a la forma de los toros. Por ejemplo: los donuts, las juntas tóricas, los salvavidas y los mangos de las tazas de café. Aunque la propiedad hueca no existe para estos objetos, el enrollamiento circular en cada ejemplo ayuda en sus escenarios específicos. Por ejemplo, la flotación de los salvavidas es posible porque su gran superficie desplaza más peso del agua que su propio peso.

Para las aplicaciones en matemáticas, se puede hacer un estudio sobre el estiramiento del material que se produce al formar un toroide. Una lámina plana puede adoptar la forma de un toro, pero distorsiona su superficie para tener en cuenta tanto la envoltura como cilindro como la flexión para unir los extremos del cilindro. La tensión del material puede estudiarse mediante la formación de un toroide para determinar si la durabilidad puede soportar tal desfiguración al comenzar como una lámina.

Torus vs. Toroide

Los dos términos se utilizan a menudo como sinónimos, pero hay una sutil diferencia.

• El toroide se produce al girar un círculo.
• Un toroide es una superficie de revolución que se obtiene al girar una curva cerrada alrededor de un eje. Un toroide puede tener cualquier forma geométrica.

Vídeos de Toro geometría