Área de un triángulo equilátero

La fórmula del área de un triángulo equilátero viene dada por:

Área del triángulo equilátero (A) = (√3/4)a2

Donde a = longitud de los lados

Derivación del área del triángulo equilátero

Hay tres métodos para derivar la fórmula del área de los triángulos equiláteros. Son:

• Usando la fórmula básica del triángulo
• Usando la construcción de rectángulos
• Utilizando la trigonometría

Deducción del área de un triángulo equilátero mediante la fórmula básica del triángulo

Tomemos un triángulo equilátero de lado "a" unidades. A continuación trazamos una bisectriz perpendicular a la base de altura "h".

Ahora,

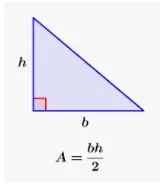
Área del triángulo = ½ × base × altura

Aquí, base = a, y altura = h

Ahora, aplica el Teorema de Pitágoras en el triángulo.

a2 = h2 + (a/2)2

⇒ h2 = a2 - (a2/4)

⇒ h2 = (3a2)/4

O bien, h = ½(√3a)

Ahora, pon el valor de "h" en la ecuación del área del triángulo.

Área del triángulo = ½ × base × altura

⇒ A = ½ × a × ½(√3a)

O bien, Área del triángulo equilátero = ¼(√3a2)

Derivación del área del triángulo equilátero mediante la construcción de un rectángulo

Considera un triángulo equilátero cuyos lados son iguales a "a".

Ahora, dibuja una línea recta desde el vértice superior del triángulo hasta el punto medio de la base del triángulo, dividiendo así la base en dos mitades iguales.

Área del triángulo equilátero

Aquí, la longitud del triángulo equilátero se considera "a" y la altura "h".

Así que el área de un triángulo equilátero = Área de un rectángulo = ½×a×h ............. (i)

La mitad del rectángulo es un triángulo rectángulo, como puede verse en la figura anterior.

Por tanto, aplicando el Teorema de Pitágoras

⇒ a2 = h2 + (a/2)2

⇒ h2 = (3/4)a2

⇒ h = (√3/2)a ...............(ii)

Sustituyendo el valor de (ii) en (i), tenemos:

Área de un triángulo equilátero

=(½)×a×(√3/2)a

=(√3/4)a2

Derivación del área de un triángulo equilátero mediante trigonometría

Si se dan dos lados de un triángulo, se puede calcular la altura mediante funciones trigonométricas. Ahora, la altura de un triángulo ABC será

h = b. Sin C = c. Sin A = a. Sin B

Ahora, el área de ABC = ½ × a × (b . sen C) = ½ × b × (c . sen A) = ½ × c (a . sen B)

Ahora, como es un triángulo equilátero, A = B = C = 60°

Y a = b = c

Área = ½ × a × (a . Sin 60°) = ½ × a2 × Sin 60° = ½ × a2 × √3/2

Por lo tanto, el área del triángulo equilátero = (√3/4)a2

¿Qué es un triángulo equilátero?

Existen principalmente tres tipos de triángulos que son los triángulos escalenos, los triángulos equiláteros y los triángulos isósceles. Un triángulo equilátero tiene los tres lados iguales y todos los ángulos iguales a 60°. Todos los ángulos de un triángulo equilátero son congruentes.

Propiedades del triángulo equilátero

Un triángulo equilátero es aquel en el que los tres lados son iguales. Es un caso especial del triángulo isósceles en el que el tercer lado también es igual. En un triángulo equilátero ABC, AB = BC = CA.

Algunas propiedades importantes de un triángulo equilátero son:

• Un triángulo equilátero es un triángulo en el que los tres lados son iguales.
• Los triángulos equiláteros también se llaman equiangulares. Es decir, los tres ángulos internos son iguales entre sí y el único valor posible es 60º cada uno.
• Es un polígono regular de 3 lados.
• Un triángulo es equilátero si y sólo si los circuncentros de tres de los triángulos más pequeños tienen la misma distancia del centroide.
• Un triángulo es equilátero si y sólo si tres de los triángulos menores tienen el mismo perímetro o el mismo radio interior.
• El área de un triángulo equilátero es básicamente la cantidad de espacio que ocupa un triángulo equilátero.
• En un triángulo equilátero, la mediana, la bisectriz del ángulo y la perpendicular son iguales y pueden denominarse simplemente bisectriz de la perpendicular debido a las condiciones de congruencia.
• El ortocentro y el centroide del triángulo son el mismo punto.
  En un triángulo equilátero, la mediana, la bisectriz del ángulo y la altura de todos los lados son iguales y son las líneas de simetría del triángulo equilátero.
• El área de un triángulo equilátero es √3 a2/ 4
• El perímetro de un triángulo equilátero es 3a.

Vídeos de Área de un triángulo equilátero