Asíntota oblicua

Las curvas visitan estas asíntotas pero nunca las sobrepasan. El método elegido para encontrar los cambios de asíntota horizontal consiste en comparar los grados de los polinomios del numerador y del denominador de la función. Si los dos polinomios tienen el mismo grado, se dividen los coeficientes de los términos de mayor grado.

Asíntotas Significado

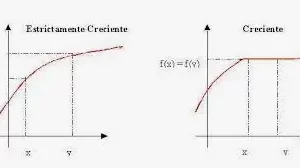
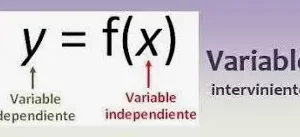
Una asíntota de la curva y = f(x) o en la forma implícita: f(x,y) = 0 es una recta tal que la distancia entre la curva y la recta se hace cero cuando los puntos de la curva se acercan al infinito.

Hay tres tipos de asíntotas, a saber

• Asíntotas verticales
• Asíntotas horizontales
• Asíntotas oblicuas

Lo que hay que tener en cuenta es que la distancia entre la curva y la asíntota tiende a ser cero cuando se acerca al infinito o al -infinito.

Las asíntotas oblicuas representan las funciones lineales que guían los comportamientos extremos de una función racional desde ambos extremos.

Aprender sobre las asíntotas oblicuas puede ayudarnos a predecir cómo se comportan las gráficas en los valores extremos.

¿Qué es una asíntota oblicua?

Las asíntotas oblicuas también se conocen como asíntotas inclinadas. Esto se debe a su forma inclinada que representa la gráfica de una función lineal, Y=mx+b. Una función racional sólo puede contener una asíntota oblicua cuando el grado de su numerador es exactamente un grado mayor que el grado de su denominador.

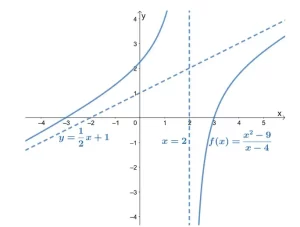
Las asíntotas oblicuas son las funciones lineales que podemos utilizar para predecir el comportamiento final de las funciones racionales, como muestra nuestro ejemplo siguiente.

Como se puede ver en el gráfico, la asíntota oblicua de 's está representada por una línea discontinua que guía el comportamiento del gráfico.

La asíntota oblicua nos da una idea de cómo se comporta la curva de al acercarse y . La gráfica de también confirma lo que ya sabemos: que las asíntotas oblicuas serán lineales (y oblicuas).

Reglas de la asíntota oblicua de las funciones racionales

Al encontrar la asíntota oblicua de una función racional, siempre nos aseguramos de comprobar los grados del numerador y del denominador para confirmar si una función tiene una asíntota oblicua. Comprueba que el grado del numerador es exactamente un grado mayor.

• Regla 1: Si el numerador es un múltiplo del denominador, la asíntota oblicua será la forma simplificada de la función.
• Regla 2: Si el numerador no es un múltiplo del denominador, utiliza la división larga o la división sintética para encontrar el cociente de la función.

Vídeos de Asintota oblicua

https://www.youtube.com/watch?v=qe0Et3YdZik