Derivadas inmediatas

Antes de pasar a la sección en la que aprendemos a calcular derivadas evitando los límites que estábamos evaluando en la sección anterior, tenemos que echar un vistazo rápido a algunas de las interpretaciones de la derivada. Todas estas interpretaciones surgen al recordar cómo surgió nuestra definición de la derivada. La definición surgió al notar que todos los problemas que trabajamos en la primera sección del capítulo de Límites requerían que evaluáramos el mismo límite.

Derivadas inmediatas

Derivada, en matemáticas, la tasa de cambio de una función con respecto a una variable. Las derivadas son fundamentales para la solución de problemas de cálculo y ecuaciones diferenciales. En general, los científicos observan sistemas cambiantes (sistemas dinámicos) para obtener la tasa de cambio de alguna variable de interés, incorporan esta información en alguna ecuación diferencial y utilizan técnicas de integración para obtener una función que pueda utilizarse para predecir el comportamiento del sistema original en diversas condiciones.

La derivada de una función describe su tasa de cambio en un punto concreto de la función. La tasa de cambio no tiene por qué ser constante, por lo que puede aproximarse a lo largo de cualquier punto de una curva. Las derivadas en el cálculo tienen muchas aplicaciones en las ciencias cuantitativas como la física y la química.

Definición geométrica

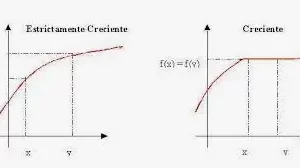
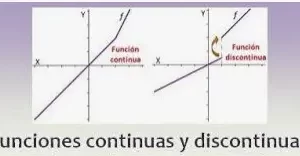
No todas las funciones son lineales. Si una función es continua, de modo que cambios muy pequeños en la entrada producen cambios en la salida, la forma de la gráfica es una curva. Para aproximar la cantidad de cambio en cualquier punto de la curva, se puede dejar caer una línea tangente. La derivada es la medida de la pendiente de la línea en ese punto.

Leer Tabla de derivadas

Diferenciación

La diferenciación es el proceso de encontrar derivadas. Tanto Newton como Leibniz utilizaron la diferenciación en el proceso de desarrollo del cálculo. La diferencial es un cambio infinitesimal en una cantidad variable, y puede relacionarse con todos los demás cambios en una función. Aunque el cambio sea infinitamente pequeño, puede medirse mediante una aproximación.

Derivadas en el espacio y el tiempo

Para medir los cambios en el espacio y el tiempo, se utilizan las derivadas en las ecuaciones diferenciales. La derivada del tiempo, o tasa de cambio en el tiempo, es importante para conceptos como la velocidad y la aceleración. (Se puede decir que Newton desarrolló el cálculo para cuantificar sus observaciones en la mecánica clásica). Por ejemplo, la velocidad es la tasa de cambio de la posición con respecto al tiempo. La aceleración es el índice de cambio de la velocidad con respecto al tiempo. No es necesariamente constante, y puede implicar ajustes minúsculos de la velocidad.

Otras aplicaciones

Las derivadas y las ecuaciones diferenciales se utilizan en las ciencias cuantitativas y en la modelización. Por ejemplo, la tasa de reacción en química es una tasa de cambio, medida por ecuaciones diferenciales. La mayoría de las medidas de comportamiento (como en psicología, sociología y economía) pueden aproximarse mediante la curva normal, que representa un cambio que es continuo pero no lineal. Muchos estudiantes de secundaria realizan pruebas estandarizadas como el SAT y el ACT. Los cambios en las puntuaciones a lo largo del tiempo pueden modelizarse mediante técnicas estadísticas avanzadas, basadas en derivadas y ecuaciones diferenciales.