Elipse fórmulas

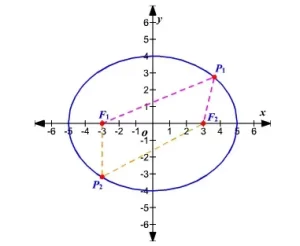
Los segmentos P F 1 ¯ y P F 2 ¯ son los radios focales de P .

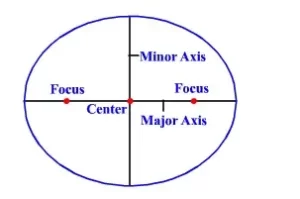
El centro de la elipse es el punto medio del segmento de línea que une sus focos. El eje mayor de la elipse es la cuerda que pasa por sus focos y tiene sus puntos extremos en la elipse. El eje menor de la elipse es la cuerda que contiene el centro de la elipse, tiene sus puntos extremos en la elipse y es perpendicular al eje mayor.

Una elipse tiene una ecuación cuadrática en dos variables.

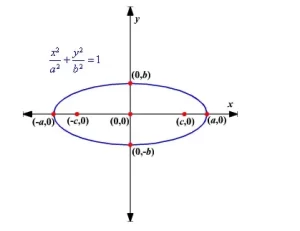
Dada una elipse con centro en ( 0 , 0 ) , focos en el eje x en ( c , 0 ) y ( - c , 0 ) , intersecciones x ( ± a , 0 ) e intersecciones x ( 0 , ± b ) . La longitud del eje mayor es 2 a y la ecuación de la elipse es

x 2 a 2 + y 2 b 2 = 1 donde b 2 = a 2 - c 2

El eje mayor está en el eje x.

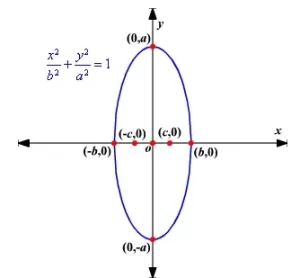
Si los focos de la elipse están en el eje y, entonces los puntos focales son ( 0 , ± c ) , y la fórmula es

x 2 b 2 + y 2 a 2 = 1 donde b 2 = a 2 - c 2

El eje mayor está en el eje y. Las intersecciones x son ( ± b , 0 ) y las intersecciones y son ( 0 , ± a ) .

Observa que el eje mayor es horizontal si el término x 2 tiene el denominador mayor y vertical si el término y 2 tiene el denominador mayor. Como el mayor de los dos denominadores es a 2 , la longitud del eje mayor es siempre 2 a y la longitud del eje menor es siempre 2 b . La distancia del centro a cualquiera de los focos es | c |.

Como el centro de cada una de estas elipses tiene su centro en el origen, se llaman elipses centrales .

Vídeos de Elipse fórmulas