Longitud de una circunferencia

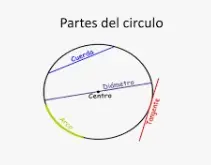
En la circunferencia dada con 'O' como centro, AB representa el diámetro del círculo (cuerda más larga), 'OE' denota el radio del círculo y CD representa una cuerda del círculo.

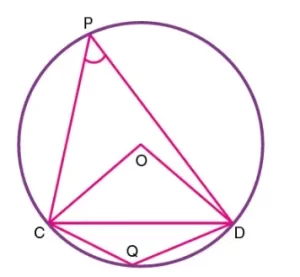
Consideremos la cuerda CD del círculo y dos puntos P y Q en cualquier lugar de la circunferencia del círculo, excepto la cuerda, como se muestra en la figura siguiente. Si los puntos extremos de la cuerda CD están unidos al punto P, entonces el ángulo ∠CPD se conoce como el ángulo subtendido por la cuerda CD en el punto P. El ángulo ∠CQD es el ángulo subtendido por la cuerda CD en Q. El ángulo ∠COD es el ángulo subtendido por la cuerda CD en el centro O.

Ángulo subtendido por la cuerda

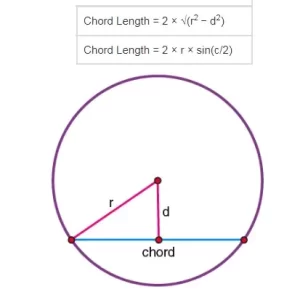
Hay dos fórmulas básicas para encontrar la longitud de la cuerda de una circunferencia que son:

Fórmula para calcular la longitud de una cuerda

Donde,

r es el radio del círculo
c es el ángulo subtendido en el centro por la cuerda
d es la distancia perpendicular de la cuerda al centro del círculo

Ejemplo de pregunta con la fórmula de la longitud de la cuerda

• Halla la longitud de la cuerda de una circunferencia cuyo radio es de 7 cm y la distancia perpendicular de la cuerda al centro es de 4 cm.

Solución:

Dado el radio, r = 7 cm

y distancia, d = 4 cm

Longitud de la cuerda = 2√(r2-d2)

⇒ Longitud de la cuerda = 2√(72-42)

⇒ Longitud de la cuerda = 2√(49-16)

⇒ Longitud de la cuerda = 2√33

⇒ Longitud de la cuerda = 2×5,744

O bien, la longitud de la cuerda = 11,48 cm

Teoremas de la cuerda de una circunferencia

Si intentamos establecer una relación entre diferentes cuerdas y el ángulo subtendido por ellas en el centro de la circunferencia, vemos que la cuerda más larga subtiende un ángulo mayor en el centro. Del mismo modo, dos cuerdas de igual longitud subtienden igual ángulo en el centro. Intentemos demostrar esta afirmación.

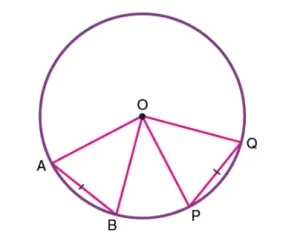
Teorema de las cuerdas iguales y los ángulos iguales

Afirmación: Las cuerdas de igual longitud subtienden ángulos iguales en el centro de la circunferencia.

Teorema de los ángulos iguales y de las cuerdas iguales (inverso del teorema 1)

Afirmación: Si los ángulos subtendidos por las cuerdas de una circunferencia son de igual medida, entonces la longitud de las cuerdas es igual.

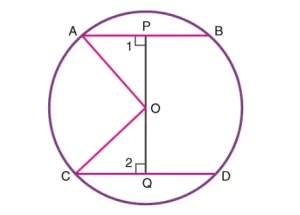
Teorema de la igualdad de las cuerdas que no distan del centro

Afirmación: Las cuerdas iguales de una circunferencia son equidistantes del centro de la misma.

Dada: Las cuerdas AB y CD son iguales en longitud.

Construcción: Unir A y C con el centro O y tirar perpendiculares desde O a las cuerdas AB y CD.

Vídeos de Longitud de una circunferencia