Máximos y mínimos

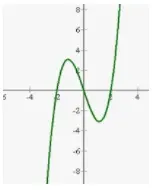
Un máximo local es un punto en el que la función es mayor en ese punto que en cualquier dirección. Es decir, tanto para valores ligeramente menores como para valores ligeramente mayores de xx la función es menor. Por lo que sabemos sobre funciones crecientes y decrecientes, esto significa que la función es creciente a la izquierda del punto y decreciente a la derecha. Estamos buscando el punto en el que la función pasa de ser creciente a decreciente, por lo que utilizamos los mismos intervalos.

Puntos críticos

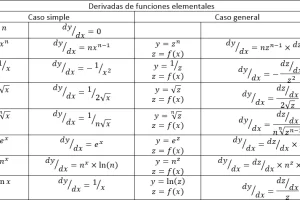
Se utiliza el mismo proceso que para encontrar intervalos crecientes y decrecientes. Toma la derivada y luego encuentra cuando la derivada es 0 o indefinida (denominador igual a 0). Asegúrate de que la derivada, y no la función original, es igual a 0. Estos son los puntos críticos que comprobaremos para los máximos y mínimos en el siguiente paso.

¿Cómo sabemos si un punto crítico es un máximo o un mínimo local?

Definimos un máximo local como un punto en el que la función pasa de ser creciente por la izquierda a ser decreciente por la derecha. Por lo tanto, si ya hemos determinado los intervalos de aumento y disminución, simplemente miramos los intervalos que rodean al punto crítico. Si pasan de ser crecientes a decrecientes, se trata de un máximo local. Si pasan de decrecientes a crecientes, se trata de un mínimo local. Si la función es creciente en ambos lados o decreciente en ambos lados, entonces la función no tiene un máximo o un mínimo en este valor crítico.

Si aún no has determinado dónde la función es creciente y decreciente, tienes dos opciones. Una es determinar estos intervalos y ver dónde la función cambia de creciente a decreciente o viceversa. La otra es la prueba de la segunda derivada.

Si la segunda derivada es positiva en el punto crítico, entonces la función es cóncava hacia arriba, por lo que la función tiene un mínimo local. Por supuesto, si la segunda derivada es negativa, la función tiene un máximo local. Aquí positivo significa mínimo y negativo significa máximo, así que para no confundirte debes pensar en cómo son las cóncavas hacia arriba y hacia abajo.

Si necesitas determinar la concavidad, entonces tendrás que encontrar la segunda derivada, así que también podrías utilizar la prueba de la segunda derivada. Si simplemente se te pide que encuentres máximos y mínimos locales entonces puedes elegir cualquiera de los dos enfoques dependiendo de con cuál te sientas más cómodo.

¿Qué es un máximo global?

Un máximo global es simplemente el mayor valor de la función en todo su dominio. Una función puede tener muchos máximos locales, pero sólo puede haber un máximo global. Como un máximo global es mayor que todo, será un máximo local, por lo que encontrar el máximo global es casi tan fácil como comprobar cada máximo local y ver cuál es el mayor.

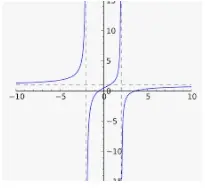
En un intervalo cerrado una función tendrá un máximo global, pero si una función tiene un dominio de todos los números reales entonces podría crecer más y más sin límite y por lo tanto no tener un máximo global. Por ejemplo, f(x)=xf(x)=x no tiene un máximo global en el dominio de todos los números reales, ya que la función puede crecer más que cualquier máximo posible. Así que tenemos que comprobar el comportamiento de la función cuando xx se acerca al infinito positivo y negativo para cualquier función con un dominio de todos los números reales.

Vídeos de maximos y minimos

https://www.youtube.com/watch?v=5XUD_Pbjskk