Volumen de un prisma pentagonal
El volumen de un prisma pentagonal = área de la base × altura
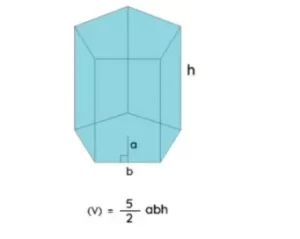
El volumen de un prisma pentagonal determina la capacidad del prisma. Según la fórmula general del volumen de un prisma, es decir, volumen = área de la base × altura. El área de la base = 1/2 × perímetro × unidades cuadradas apotema, donde el perímetro = 5b. Así, la fórmula del volumen de un prisma pentagonal es Volumen = (5/2 × abh) unidades cúbicas donde,
a = Longitud apotema del prisma pentagonal
b = Longitud de la base del prisma pentagonal
h = Altura del prisma pentagonal
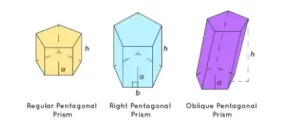
Dado que la tercera dimensión de las medidas ha entrado en escena, la unidad será unidades cúbicas como estos centímetros cúbicos. Hay tres tipos de prismas pentagonales: prismas pentagonales regulares, prismas pentagonales rectos y prismas pentagonales oblicuos.
Volumen del prisma pentagonal según los tipos de prismas pentagonales
- En el caso de un prisma pentagonal regular, las dos caras pentagonales tienen la misma longitud y las cinco caras rectangulares con bases son perpendiculares entre sí.
- En el caso de un prisma pentagonal recto, las bases son perpendiculares entre sí.
- En el caso de un prisma pentagonal oblicuo, las bases no son perpendiculares entre sí. Por tanto, la perpendicular trazada desde un vértice de una base a la otra base del prisma se tomará como su altura.
¿Cómo se calcula el volumen de un prisma pentagonal?
Estos son los pasos para calcular el volumen de un prisma pentagonal. Debemos asegurarnos de que todas las medidas son de las mismas unidades. Consulte el ejemplo que se da a continuación seguido de los pasos.
- Paso 1: Identificar la longitud de la apotema y la longitud de la base y encontrar su área utilizando una fórmula adecuada (área de la base= 5/2ab).
- Paso 2: Identificar la altura dada del prisma (debe ser la altura del prisma total).
- Paso 3: Hallar el producto del área de la base por la altura para hallar el volumen.
Ejemplo: Calcular el volumen del prisma pentagonal si la longitud de la apotema "a" de un prisma pentagonal es de 5 pies, la longitud de la base "b" es de 4 pies, y la altura "h" es de 6 pies.
Solución: Dado que a = 5 pies, b = 4 pies y h = 6 pies. El volumen del prisma pentagonal se obtiene mediante la fórmula V = 5/2 × abh. Los pasos para determinar el volumen del prisma pentagonal son:
- Paso 1: El área de la base del prisma pentagonal se encuentra utilizando la fórmula, 5/2ab = 5/2 × 5 × 4 = 50 pies cuadrados.
- Paso 2: La altura del prisma es de 6 pies.
- Paso 3: El volumen del prisma pentagonal = área de la base × altura = 50 × 6 = 300 pies cúbicos.
Por lo tanto, el volumen del prisma pentagonal es de 300 pies cúbicos.