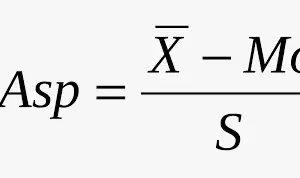¿Qué es una medida de tendencia no central?

La mediana es el percentil 50. La mitad de los valores son más altos y la otra mitad más bajos. Ordena los valores de menor a mayor. Si hay un número impar de puntos, la mediana es el que está en el medio. Si hay un número par de puntos, la mediana es la media de los dos valores del medio.

Cuartiles

Los cuartiles dividen los datos en cuatro grupos, cada uno de los cuales contiene un número igual de valores. Los cuartiles se dividen por los percentiles 25, 50 y 75, también llamados primer, segundo y tercer cuartil. Un cuarto de los valores es menor o igual que el percentil 25. Tres cuartas partes de los valores son inferiores o iguales al percentil 75.

Rango intercuartil

La diferencia entre el percentil 75 y el 25 se denomina rango intercuartílico. Es una forma útil de cuantificar la dispersión.

Cálculo de percentiles

Calcular un percentil distinto de la mediana no es sencillo. Lo creas o no, existen al menos ocho métodos diferentes para calcular los percentiles. Aquí hay otra explicación de los diferentes métodos (desplácese hacia abajo hasta "trazar posiciones").

Prism calcula los valores de los percentiles evaluando primero esta expresión

R = P * (n + 1)/100

P es el percentil deseado (25 o 75 para los cuartiles) y n es el número de valores del conjunto de datos. El resultado es el rango que corresponde al valor del percentil. Si hay 68 valores, el percentil 25 corresponde a un rango igual a

0.25 * 69 = 17.25

Prism (desde la versión 5) interpola un cuarto del camino entre el valor 17 y el 18. Este es el método más utilizado en los programas estadísticos. Es la definición 6 de Hyndman y Fan (1) . Con este método, el percentil de cualquier punto es k/(n+1), donde k es el rango (empezando por 1) y n es el tamaño de la muestra. Esta no es la misma forma en que Excel calcula los percentiles, por lo que los percentiles calculados por Prism y Excel no coincidirán cuando el tamaño de la muestra sea pequeño.

Tenga cuidado con los percentiles de conjuntos de datos pequeños. Considere este ejemplo: ¿Cuál es el percentil 90 de seis valores? Utilizando la fórmula anterior, R es igual a 6,3. Como el valor más grande tiene un rango de 6, no es posible calcular el percentil 90. Prism reporta el valor más grande como el percentil 90. Un problema similar ocurre si se intenta calcular el percentil 10 de seis valores. R es igual a 0,7, pero el valor más bajo tiene un rango de 1. Prism informa del valor más bajo como el 10º percentil.

Observe que no hay ninguna ambigüedad sobre cómo calcular la mediana. Todas las definiciones de percentiles conducen al mismo resultado para la mediana.

Vídeos de ¿Qué es una medida de tendencia no central?