Tasa de variación fórmula

La tasa de cambio es el cambio de una variable en relación con el cambio de otra variable. Una tasa de cambio común es la velocidad, que mide el cambio en la distancia recorrida en relación con el tiempo transcurrido. El medallista de oro olímpico Usain Bolt se convirtió en el hombre más rápido del mundo al correr a una velocidad máxima de 44,72 km/h en los 100 metros lisos. En promedio, su velocidad fue un poco más lenta (no obstante, muy impresionante) con 37,58 km/h. La velocidad máxima de Bolt es un ejemplo de tasa de cambio instantánea, y su velocidad media es una tasa de cambio promedio.

Tasa de variación media

Las rectas secantes se encuentran conectando dos puntos de una curva. La pendiente de la línea secante entre dos puntos representa la tasa de cambio promedio en ese intervalo.

En matemáticas, una tasa de cambio es una expresión matemática que relaciona los cambios en una cantidad con los cambios en otra cantidad. Las tasas de cambio son útiles para describir cómo los sistemas cambian con el tiempo y cómo un cambio en una variable afecta al cambio en otra. Las tasas de cambio son útiles en varios campos en los que se utilizan para resumir una relación entre dos variables.

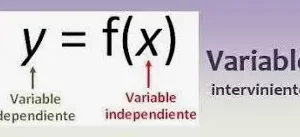
Un ejemplo sencillo de tasa de cambio es la velocidad. En esencia, la velocidad es un índice de cambio. En concreto, la velocidad describe un cambio en la distancia con respecto a un cambio en el tiempo. Una velocidad de 3 m/s nos dice que el desplazamiento de un objeto cambia en 3 metros por cada 1 segundo. Por cada cambio en la variable independiente (tiempo), la variable dependiente (distancia) cambia 3 metros.

Las tasas de cambio son especialmente útiles en el álgebra, el cálculo y la física, ya que estos campos tratan habitualmente con sistemas complejos en los que los cambios continuos en una variable se correlacionan con los cambios en otra. Las tasas de cambio nos permiten describir y predecir cómo cambian dos cantidades entre sí.

Vídeos de Tasa de variación fórmula

https://www.youtube.com/watch?v=E9e7-NxFFcg